All the surfaces shown in figure are assumed to be frictionless. The block of mass m slides on the prism which in turn slides backward on the horizontal surface. Find the acceleration of the smaller block with respect to the prism.

Let a0 be the acceleration of prism in the backward direction . The mass .m. is placed on non - inertial frame , therefore it is acted on by fictitious force ma0 in the forward direction . The forces acting on mass m are
(i) Weight mg acting downward,
(ii) Normal reaction R,
(iii) Fictitious force ma0.
According free body diagram of .m. is shown in figure .
Suppose block m slides down the prism with acceleration a .
The equation of motion of .m. parallel to incline is
ma0cosθ+mgsinθ ....(1)
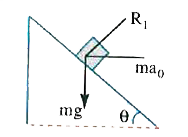
The block is in equilibrium perpendicular to incline , so resolving force perpendicular to incline
R1+ma0sinθ=mgcosθ ....(2)
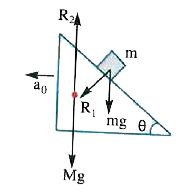
Now we consider the forces acting on the prism . As prism is on ground (inertial frame ) no fectitious force acts on it . The forces on prism are
(i) Weight (Mg) downward.
(ii) Normal force R1 exerted by block
(iii) Normal reaction R2 exerted by ground .
For horizontal motion of prism
R1sinθ=MA0⇒R1=Ma0sinθ ....(3)
substituting this value in (2) ,
Ma0sinθ+ma0sinθ=mgcosθ
This gives a0=mgsinθcosθM+msin2θ ....(4)
∴ From (1) , a=mgsinθcos2θM+msin2θ+gsinθ
=(M+m)gsinθM+msin2θ
Similar Questions
A force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
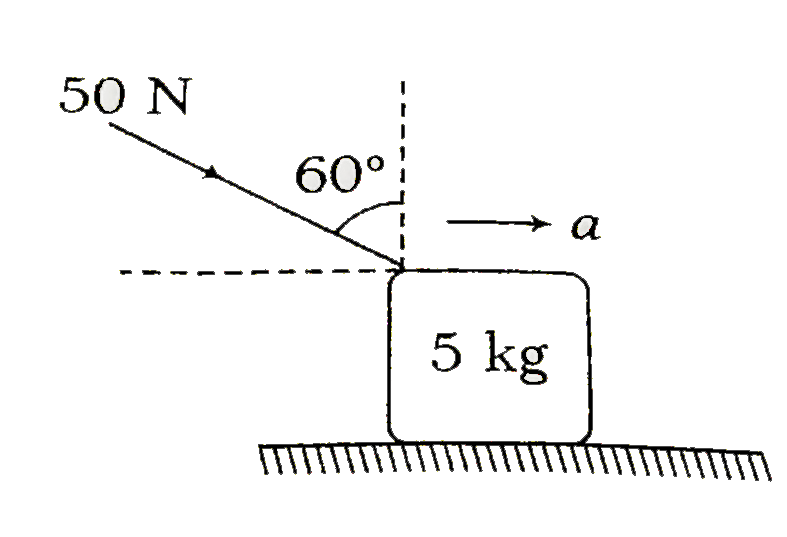
View SolutionA force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.

View Solution
Knowledge Check
Assuming all the surface to be frictionless. The smaller block m is moving horizontally with acceleration a and vertically downwards with acceleration a. Then magnitude of net acceleration of smaller block m with respect to ground
 A2√5mg(5m+M)B2mg(5m+M)C7√5gDnone of these
A2√5mg(5m+M)B2mg(5m+M)C7√5gDnone of these
A block slides down a frictionless, inclined plane that makes a 30∘ angle with the horizontal. Find the acceleration of this block.
View SolutionA block of mass m is kept over another block of mass M and the system rests on a horizontal surface. A constant horizontal force F acting on the lower block produces an acceleration F2(m+M) in the sytem. The two blocks always move together. Consider displacement d of the system.
a. Find the work done by friction on bigger block.
b. Find the coefficient of kinetic friction between the bigger block and the horizontal surface.
c. Find the frictional acting on the smaller block.
d. Find the work done by the force of friction on the smaller block by the bigger block.
e. Find the work done by static friction on bigger block.
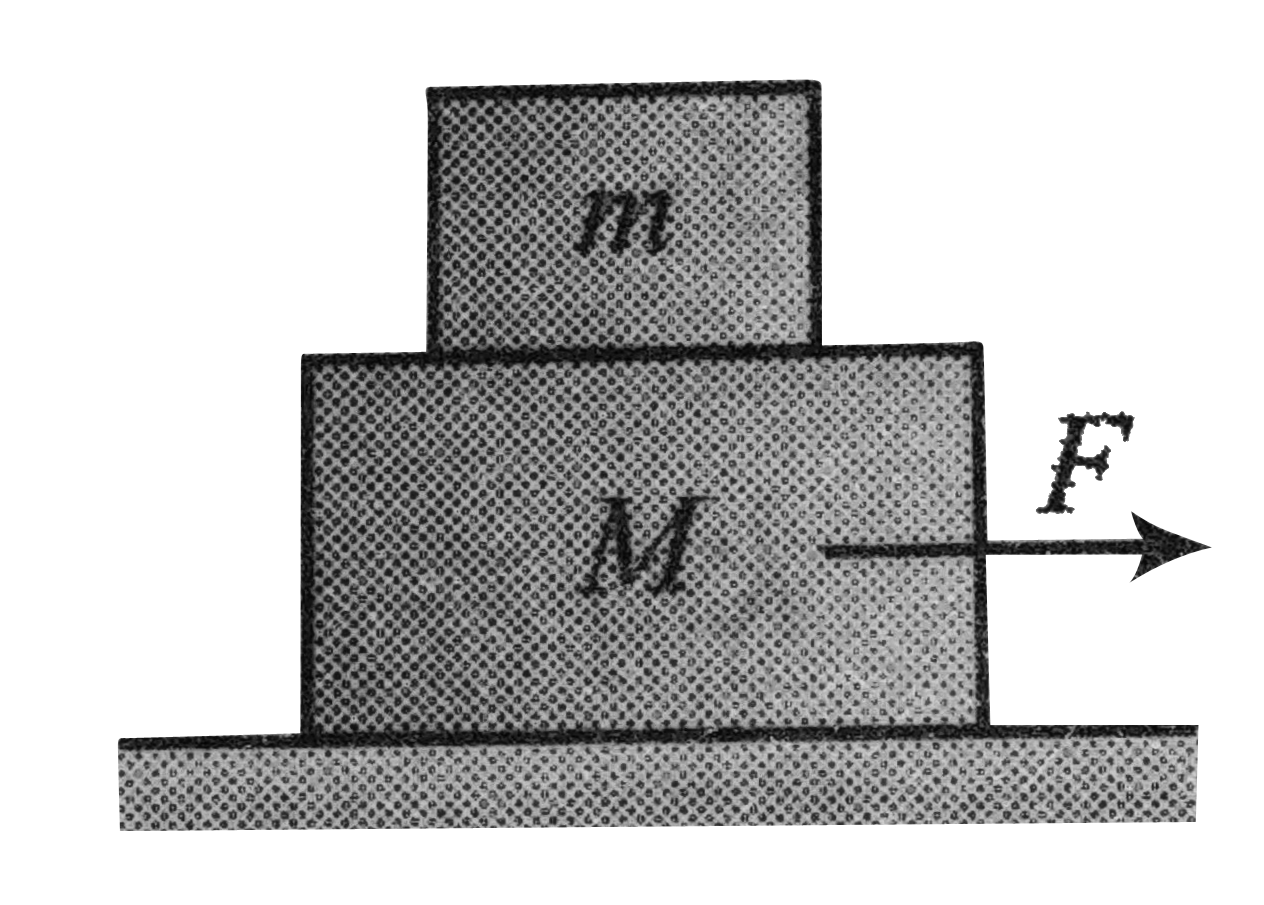
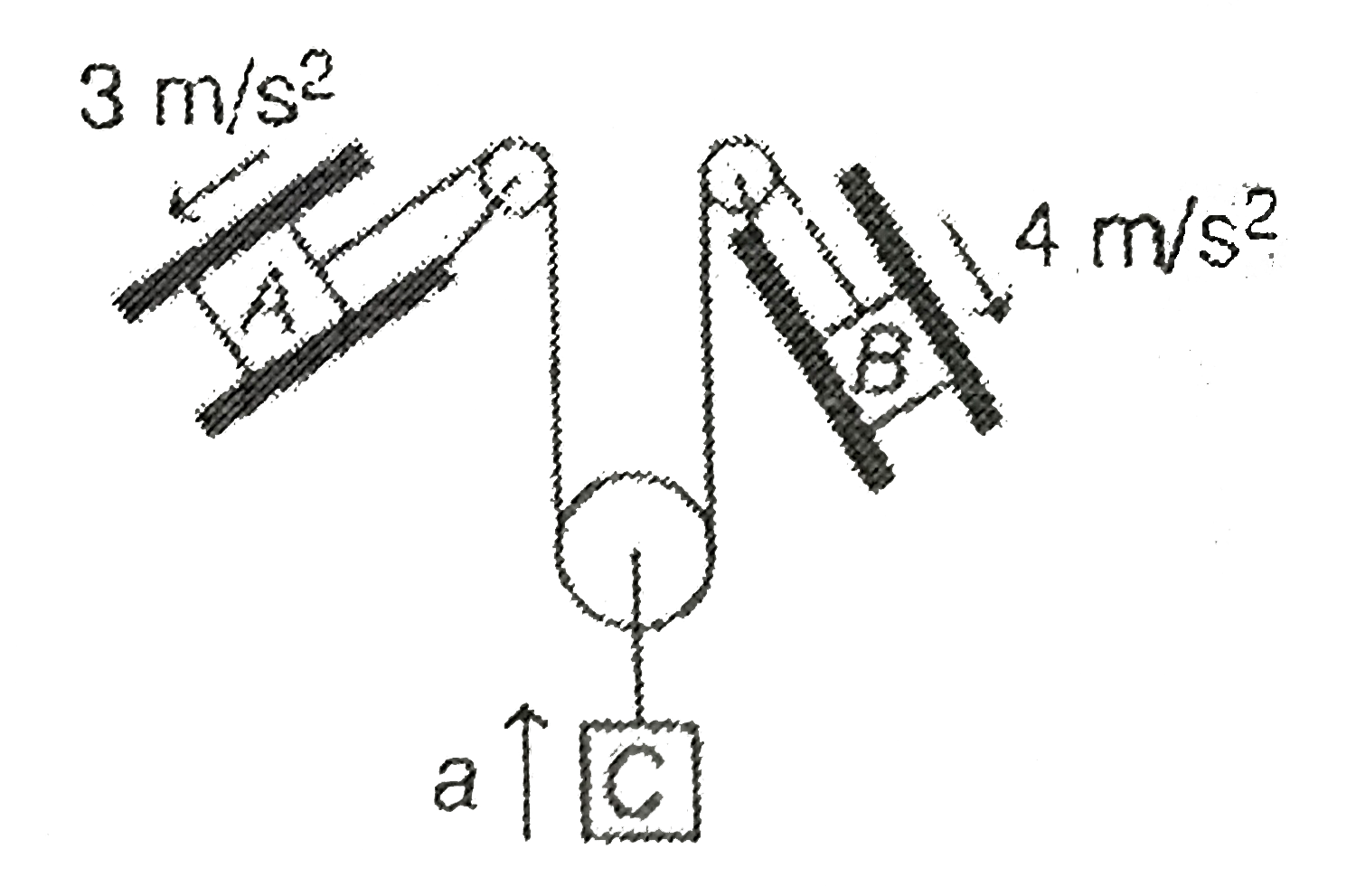
View SolutionAssuming all the surfaces to be frictionless accelration of the block c shown in the figure is
View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View SolutionA block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.

View SolutionA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-

View Solution
