Rain drops are falling vertically downward with a velocity 4kmph. The velocity with which they appear to fall down to a man travelling at 2 kmph horizontal is
√12 kmph
2√5 kmph
5 kmph
2 kmph
The correct Answer is:B
To solve the problem, we need to find the apparent velocity of the raindrops as observed by a man moving horizontally. Here’s a step-by-step solution:
Step 1: Understand the velocities involved
- The raindrops are falling vertically downward with a velocity Vr=4km/h.
- The man is moving horizontally with a velocity Vm=2km/h.
Step 2: Set up the vector components
- The velocity of the rain can be represented as a vector pointing downward (negative y-direction).
- The velocity of the man can be represented as a vector pointing horizontally (positive x-direction).
Step 3: Use the Pythagorean theorem
Since the rain is falling vertically and the man is moving horizontally, we can treat these two velocities as perpendicular components of a right triangle. The apparent velocity of the rain with respect to the man can be calculated using the Pythagorean theorem:
Vrm=√V2r+V2m
Step 4: Substitute the values
Now we substitute the given values into the equation:
Vrm=√(4km/h)2+(2km/h)2
Vrm=√16+4=√20
Step 5: Simplify the result
We can simplify √20:
Vrm=√4×5=2√5km/h
Conclusion
The velocity with which the raindrops appear to fall down to the man is 2√5km/h.
Final Answer
The correct option is 2√5km/h.
---
- The raindrops are falling vertically downward with a velocity Vr=4km/h.
- The man is moving horizontally with a velocity Vm=2km/h.
- The velocity of the rain can be represented as a vector pointing downward (negative y-direction).
- The velocity of the man can be represented as a vector pointing horizontally (positive x-direction).
Since the rain is falling vertically and the man is moving horizontally, we can treat these two velocities as perpendicular components of a right triangle. The apparent velocity of the rain with respect to the man can be calculated using the Pythagorean theorem:
Now we substitute the given values into the equation:
We can simplify √20:
The velocity with which the raindrops appear to fall down to the man is 2√5km/h.
The correct option is 2√5km/h.
Similar Questions
Raindrops are falling vertically with a velocity 10m/s. To a cyclist moving on a straight road the rain drops appear to be coming with a velocity of 20m/s. The velocity of cyclist is :-
View SolutionA small ball falling vertically downward with constant velocity 4m/s strikes elastically a massive inclined cart moving with velocity 4m/s horizontally as shown. The velocity of the rebound of the ball is
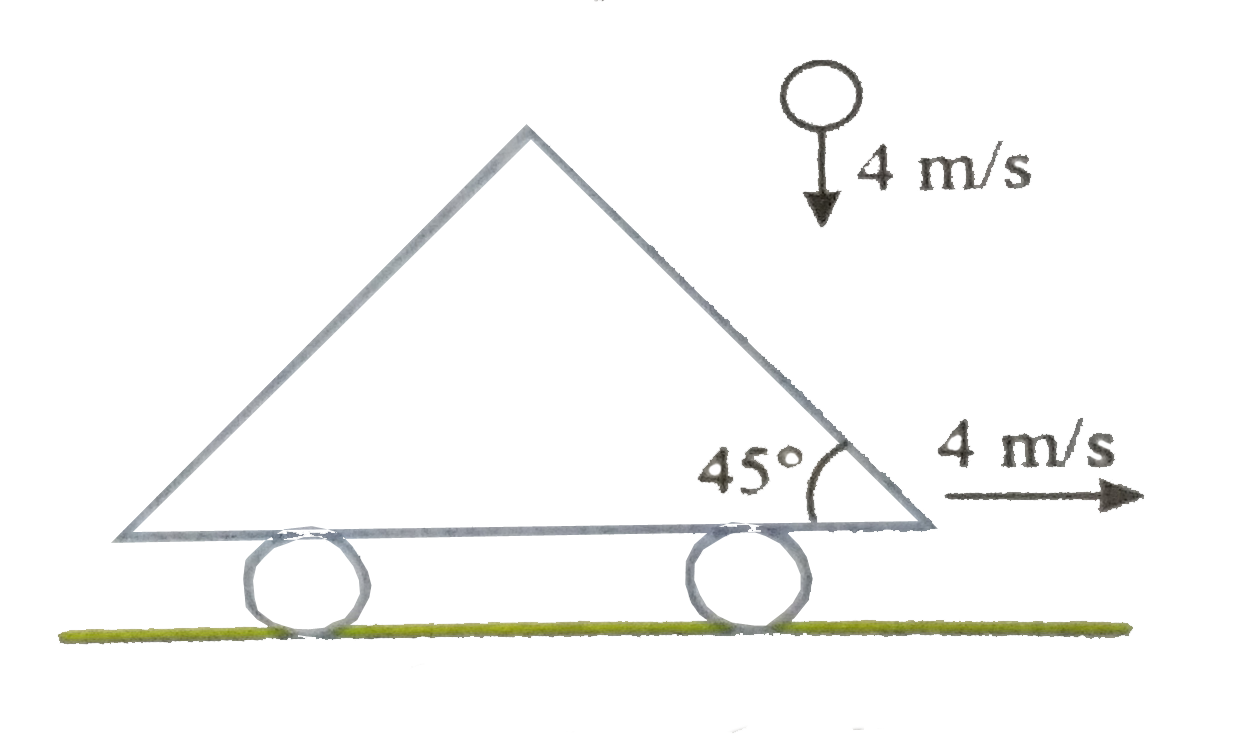
View SolutionAn object is falling vertically downwards with velocity 10m/s.In terms ofˆiandˆj find the image velocity. M

View SolutionRain is falling vertically downward with velocity 4m/s. A man is moving horizontally with velocity 3m/s, the velocity of rain with respect to man is
View SolutionRain droplets are falling in vertically downward direction with velocity 5m/s. A cyclist is moving in northward direction with velocity 10 m/s. The rain droplets will appear to the cyclist to be coming from
View SolutionRain is falling vertically and a man is moving with velocity 6m/s find the angle with which umbrella should be held by man to avoid getting wet .

View SolutionRaindrops are falling with velocity 10√2 m/s making and angle 45∘ with the vertical. The drops appear to be falling vertically to a man running with constant velocity . The velocity of rain drops change such that the rain drops now appear to be falling vertically with √3 times the velcoity it appeared earlier to the same person running with same velocity .
After the velocity of rain drops change the magnitude of velocity of raindrops with respect to ground is
View SolutionRaindrops are falling with velocity 10√2 m/s making and angle 45∘ with the vertical. The drops appear to be falling vertically to a man running with constant velocity . The velocity of rain drops change such that the rain drops now appear to be falling vertically with √3 times the velcoity it appeared earlier to the same person running with same velocity .
The angle ( in degrees) between the initial and final velocity of rain drops with respect to ground.
View SolutionRaindrops are falling with velocity 10√2 m/s making and angle 45∘ with the vertical. The drops appear to be falling vertically to a man running with constant velocity . The velocity of rain drops change such that the rain drops now appear to be falling vertically with √3 times the velcoity it appeared earlier to the same person running with same velocity .
The magnitude of velocity of man w.r.t ground is
View SolutionRain is falling vertically downwards with a velocity of 2m//s. A person is runing to the North with a velocity of 2√3m/s. Find out the velocity and direction of rain as appeared to the person.
View Solution
