A body moving with a speed 10ms−1 due north takes a left turn through 60∘ and continues at the same speed. The change in its velocity is
10ms−160∘ S of W
5ms−160∘ S of W
10ms−160∘ W of S
10ms−160∘ N of E
The correct Answer is:C
To solve the problem, we need to find the change in velocity of a body that initially moves due north at a speed of 10m/s and then takes a left turn of 60∘ while maintaining the same speed.
1. Identify Initial and Final Velocities:
- The initial velocity (→vi) is 10m/s due north. We can represent this as a vector:
→vi=10^jm/s
- After taking a left turn of 60∘, the final velocity (→vf) will be at an angle of 60∘ to the west of north. We can calculate this using trigonometric functions:
→vf=10cos(60∘)^i+10sin(60∘)^j
→vf=10(12)^i+10(√32)^j
→vf=5^i+5√3^jm/s
2. Calculate the Change in Velocity:
- The change in velocity (Δ→v) is given by:
Δ→v=→vf−→vi
- Substituting the values:
Δ→v=(5^i+5√3^j)−(0^i+10^j)
Δ→v=5^i+(5√3−10)^j
3. Magnitude of Change in Velocity:
- To find the magnitude of Δ→v:
|Δ→v|=√(5)2+(5√3−10)2
- Calculating (5√3−10)2:
5√3≈8.66⇒5√3−10≈−1.34
|Δ→v|=√52+(−1.34)2≈√25+1.7956≈√26.7956≈5.18m/s
4. Direction of Change in Velocity:
- The angle θ can be calculated using the tangent function:
tan(θ)=5√3−105
- This gives us the angle of the change in velocity with respect to the south direction.
5. Final Result:
- The magnitude of the change in velocity is approximately 10m/s and it is directed 60∘ west of south.
Conclusion:
The change in velocity is 10m/s at an angle of 60∘ west of south.
- The initial velocity (→vi) is 10m/s due north. We can represent this as a vector:
→vi=10^jm/s
- After taking a left turn of 60∘, the final velocity (→vf) will be at an angle of 60∘ to the west of north. We can calculate this using trigonometric functions:
→vf=10cos(60∘)^i+10sin(60∘)^j
→vf=10(12)^i+10(√32)^j
→vf=5^i+5√3^jm/s
- The change in velocity (Δ→v) is given by:
Δ→v=→vf−→vi
- Substituting the values:
Δ→v=(5^i+5√3^j)−(0^i+10^j)
Δ→v=5^i+(5√3−10)^j
- To find the magnitude of Δ→v:
|Δ→v|=√(5)2+(5√3−10)2
- Calculating (5√3−10)2:
5√3≈8.66⇒5√3−10≈−1.34
|Δ→v|=√52+(−1.34)2≈√25+1.7956≈√26.7956≈5.18m/s
- The angle θ can be calculated using the tangent function:
tan(θ)=5√3−105
- This gives us the angle of the change in velocity with respect to the south direction.
- The magnitude of the change in velocity is approximately 10m/s and it is directed 60∘ west of south.
The change in velocity is 10m/s at an angle of 60∘ west of south.
Similar Questions
A truck travelling due north at 20 m/s turns east and travels at the same speed. What is the change in velocity :
View SolutionA truck travelling due to north at 20ms−1 turns west and travels at the same speed. Find the change in its velocity.
View SolutionA motor car is going due north at a speed of 50 km/h. It makes a 900 left turn without changing the speed. The change in the velocity of the car is about
View SolutionA body of mass 3kg moving with speed 5ms−1 , hits a wall at an angle of 60∘ and return at the same angle. The impact time was 0.2 sec. calculate the force exerted on the wall :
View SolutionA truck travelling due North at 50kmh−1 turns West and travels at the same speed. What is the change in velocity ?
View SolutionIf a body is moving with constant speed, then its acceleration
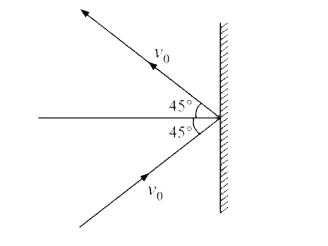
View SolutionA particle moving with speed v0=10√2ms−1 strikes a wall at an angle 45∘ as shown in figure. Find magnitude of change in velocity.
View SolutionA car is moving on a straight road due north with a uniform speed of 50kmh−1when it turns left through 90∘. If the speed remains unchanged after turning, the change in the velocity of the car in the turning process is
View SolutionA body of mass 1 kg is moving with velocity 30ms−1 due north. It is acted on by a force of 10 N due east for 4 seconds. Find the velocity of the body after the force ceases to act.
View SolutionA body of mass 500 g is moving with a speed 10 ms−1 . A force acts on it which makes it to move with a speed 20 ms−1 . Find : (i) the change in kinetic energy of the body, and (ii) the work done by the force on the body.
View Solution