A body falls from height h. The v−s graph is :
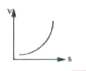

The correct Answer is:C
To solve the problem of determining the correct v-s (velocity-displacement) graph for a body falling from a height h, we can follow these steps:
Step 1: Understand the motion of the body
When a body falls freely under the influence of gravity, its motion can be described using the equations of motion. The initial velocity u is 0 (since it starts from rest), and the acceleration a is equal to g (acceleration due to gravity).
Step 2: Apply the equation of motion
We can use the equation of motion:
v2=u2+2as
Substituting u=0 and a=g:
v2=0+2gs
This simplifies to:
v2=2gs
Step 3: Differentiate the equation
To find the relationship between v and s, we differentiate v2=2gs with respect to s:
d(v2)ds=2g
Using the chain rule, we have:
2vdvds=2g
Dividing both sides by 2:
vdvds=g
Step 4: Rearrange the equation
Rearranging gives us:
dvds=gv
Step 5: Analyze the relationship
This equation shows that the change in velocity with respect to displacement dvds is inversely proportional to the velocity v. This means that as the velocity increases, dvds decreases.
Step 6: Determine the shape of the graph
Since dvds is inversely proportional to v, the slope of the v-s graph decreases as v increases. Therefore, the correct v-s graph will be one that has a decreasing slope.
Conclusion
From the options provided, the graph that shows a decreasing slope as velocity increases is the correct answer. Thus, the correct option is option 3.
---
When a body falls freely under the influence of gravity, its motion can be described using the equations of motion. The initial velocity u is 0 (since it starts from rest), and the acceleration a is equal to g (acceleration due to gravity).
We can use the equation of motion:
v2=u2+2as
Substituting u=0 and a=g:
v2=0+2gs
This simplifies to:
v2=2gs
To find the relationship between v and s, we differentiate v2=2gs with respect to s:
d(v2)ds=2g
Using the chain rule, we have:
2vdvds=2g
Dividing both sides by 2:
vdvds=g
Rearranging gives us:
dvds=gv
This equation shows that the change in velocity with respect to displacement dvds is inversely proportional to the velocity v. This means that as the velocity increases, dvds decreases.
Since dvds is inversely proportional to v, the slope of the v-s graph decreases as v increases. Therefore, the correct v-s graph will be one that has a decreasing slope.
From the options provided, the graph that shows a decreasing slope as velocity increases is the correct answer. Thus, the correct option is option 3.
Similar Questions
A body freely falling from a height h describes 11h36 in the last second of its fall. The height h is (g=10ms−2)
View SolutionA body freely falling from a height h describes 7h16 in the last second of its fall. The height h is (g=10ms−2)
View SolutionA body of mass m falls from height h, on the ground, If e is the coefficient of restitution between body and the ground, then the height upto which it rises after ten collisions is
View SolutionA body falls from a height h=200m (at New Delhi). The ratio of distance travelled in each 2sec during t=0 to t=6 seconds of the journey is.
View SolutionA body falls freely from a height 'h' after two seconds if accelaration due to gravity is reversed the body
View SolutionA body falls freely from a height 'h' after two seconds if we assume that gravity disappears the body
View SolutionA body of mass m falls from a height h1 and rises to a height h2. The magnitude of the change in momentum during the impact with the ground.
View SolutionA body falls freely from a height 'h' its average velocity when it reaches earth is
View SolutionA cage of mass M hangs from a light spring of force constant k. A body of mass m falls from height h inside the cage and stricks to its floor. The amplitude of oscillations of the cage will be-
_E01_061_Q01.png)
View SolutionA body is falling from height 'h' it takes t1 time to reach the ground. The time taken to cover the first half of height is:-
View Solution
