The coefficient of friction between the board and the floor shown in figure is μ. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor.

Let T is the force exerted by man on the rope.
Along vertical direction, ∑Fv=0,
or N+T=(M+m)g or N=(M+m)g−T The board will not slip over the floor, if T≤f.
For maximum value of T, we have
T=f=μN
=μ[(M+m)g−T]
=μ(M+m)g−μT
or T=[μ(M+m)g1+μ]
Similar Questions
The friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionThe friction coeficient bettween the board and the floor shownin filgure is μ. Find the maximum force that the man can exert on the rope so tht the board does not slipon the floor.

View Solution
Knowledge Check
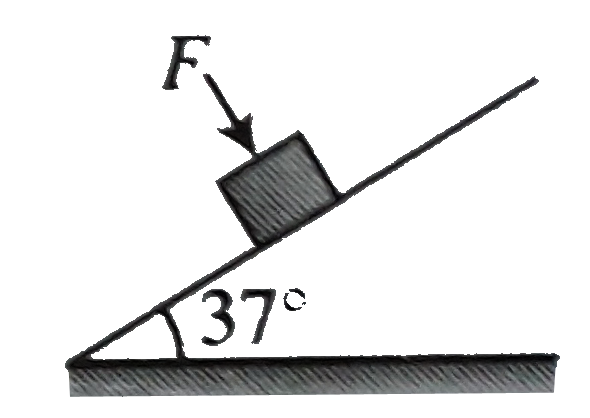
A block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 NThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 A0.15mgB0.05mgC0.1mgD0.45mg
A0.15mgB0.05mgC0.1mgD0.45mg
Find the force of friction acting between both the blocks shown in the figure.
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?
View SolutionIf the coefficient of friction between the wedge A and block B shown in the figure is μ, then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = 45∘ ]

View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=0.3, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View Solution
Consider the figure shown here of a moving cart C. if the coefficient of friction between the block A and the cart is μ, then calculate the minimum acceleration a of the cart C so that the block A does not fall.
View Solution