¯r=2¯i+3¯j−6¯k then find |¯r|.
The correct Answer is:7
To find the modulus of the vector ¯r=2¯i+3¯j−6¯k, we can follow these steps:
Step 1: Identify the components of the vector
The vector ¯r can be expressed in terms of its components:
- x=2 (coefficient of ¯i)
- y=3 (coefficient of ¯j)
- z=−6 (coefficient of ¯k)
Step 2: Write the formula for the modulus of a vector
The modulus (or magnitude) of a vector ¯r=x¯i+y¯j+z¯k is given by the formula:
|¯r|=√x2+y2+z2
Step 3: Substitute the values of x, y, and z
Substituting the values we identified:
|¯r|=√(2)2+(3)2+(−6)2
Step 4: Calculate the squares of the components
Calculating each term:
- 22=4
- 32=9
- (−6)2=36
Step 5: Add the squared values
Now, add these squared values together:
|¯r|=√4+9+36
|¯r|=√49
Step 6: Calculate the square root
Finally, calculate the square root:
|¯r|=7
Thus, the modulus of the vector ¯r is 7.
---
The vector ¯r can be expressed in terms of its components:
- x=2 (coefficient of ¯i)
- y=3 (coefficient of ¯j)
- z=−6 (coefficient of ¯k)
The modulus (or magnitude) of a vector ¯r=x¯i+y¯j+z¯k is given by the formula:
|¯r|=√x2+y2+z2
Substituting the values we identified:
|¯r|=√(2)2+(3)2+(−6)2
Calculating each term:
- 22=4
- 32=9
- (−6)2=36
Now, add these squared values together:
|¯r|=√4+9+36
|¯r|=√49
Finally, calculate the square root:
|¯r|=7
Similar Questions
Show that points with p.v ¯a−2¯b+3¯c,−2¯a+3¯b−¯c,4¯a−7¯b+7¯c are collinear. It is given that vectors ¯a,¯b,¯c are non-coplanar.
View SolutionIn a regular hexagon ABCDEF,¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=k¯¯¯¯¯¯AD then k is equal to
View SolutionA force 2¯i+¯j−¯k Newton acts on a body which is initially at rest . At the end of 20 seconds the velocity of the body is 4¯i+2¯j−2¯k m/s . What is the mass of the body ?
View SolutionEvaluate 3.¯2−0.¯¯¯¯16
View Solution(¯a⋅¯i)2+(¯a⋅¯j)2+(¯a⋅¯k)2=
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionA : The poynting vector given as ¯¯¯S=¯¯¯Eׯ¯¯Bμ0 represents the instantaneous intensity at a point.
R : The velocity of an electromagnetic wave is in the direction of the vector ¯¯¯Eׯ¯¯B.
View SolutionExpress each of the following recurring decimals into the rational number :
(i)0.¯7 (ii)0.¯6 (iii)1.¯3 (iv)3.¯8
View Solution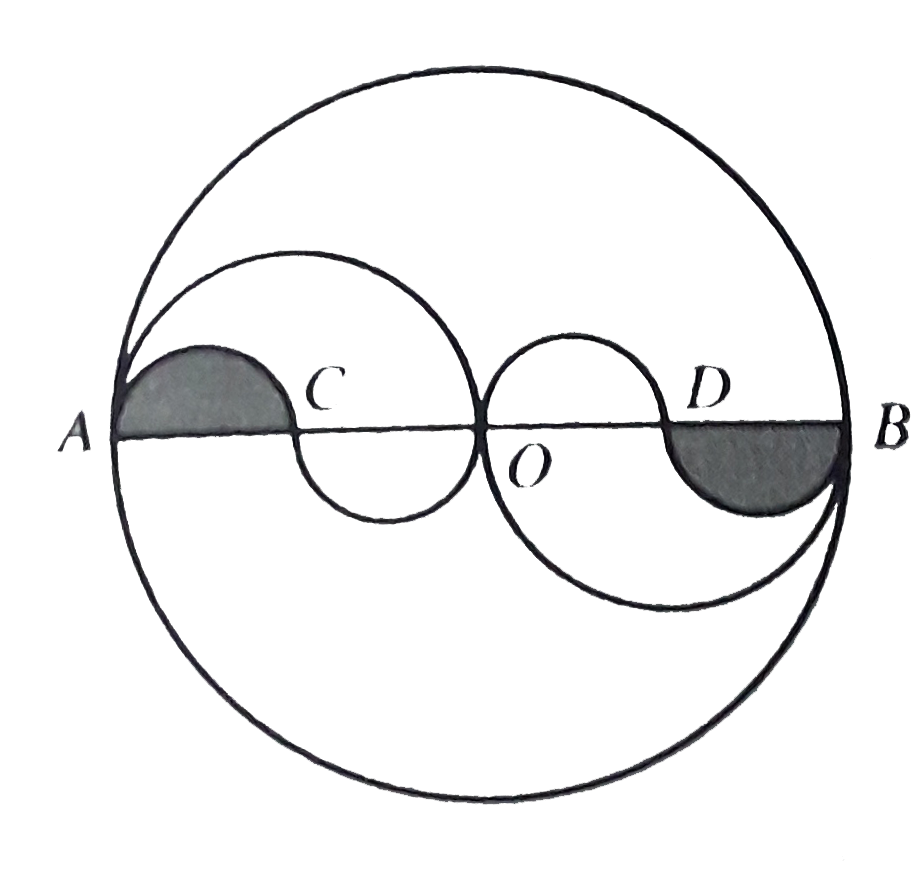
In the circle shown above, O is the center and ¯¯¯¯¯¯AB is a diameter . There are two semicircles with diameters ¯¯¯¯¯¯AO and ¯¯¯¯¯¯BO , and four smaller semicircles with congruent diameters ¯¯¯¯¯¯AC,¯¯¯¯¯¯CO,¯¯¯¯¯¯OD and ¯¯¯¯¯¯DB . A point is picked at random in the large circle . What is the probability that it lands in a shaded region ?
View SolutionExpress each of the following recurring decimals into the rational number :
(i)0.¯5 (ii)2.¯4 (iii)1.¯¯¯¯12 (iv)2.7¯¯¯¯39 (v)0.¯¯¯¯¯¯516 (vi)3.7¯¯¯¯¯¯148
View Solution

