Equation of the locus of the centroid of the triangle whose vertices are (acosk,asink),(bsink,−bcosk)and(1,0) , where k is a perameter, is
The correct Answer is:a2+b2
To find the equation of the locus of the centroid of the triangle with vertices (acosk,asink), (bsink,−bcosk), and (1,0), we will follow these steps:
Step 1: Define the Centroid
The centroid G of a triangle with vertices (x1,y1), (x2,y2), and (x3,y3) is given by the formula:
G(x,y)=(x1+x2+x33,y1+y2+y33)
For our triangle, the vertices are:
- (x1,y1)=(acosk,asink)
- (x2,y2)=(bsink,−bcosk)
- (x3,y3)=(1,0)
Step 2: Calculate the Coordinates of the Centroid
Using the centroid formula:
x=acosk+bsink+13
y=asink−bcosk+03
Step 3: Rearranging the Equations
We can rearrange the equations for x and y:
3x=acosk+bsink+1(1)
3y=asink−bcosk(2)
Step 4: Isolate cosk and sink
From equation (1):
acosk+bsink=3x−1(3)
From equation (2):
asink−bcosk=3y(4)
Step 5: Square and Add the Equations
Now, we will square equations (3) and (4) and add them:
(acosk+bsink)2+(asink−bcosk)2=(3x−1)2+(3y)2
Expanding both sides:
a2cos2k+2abcosksink+b2sin2k+a2sin2k−2absinkcosk+b2cos2k=(3x−1)2+(3y)2
Step 6: Combine Like Terms
Combining the terms gives:
a2(cos2k+sin2k)+b2(sin2k+cos2k)=(3x−1)2+(3y)2
Using the identity cos2k+sin2k=1:
a2+b2=(3x−1)2+(3y)2
Step 7: Final Equation of the Locus
Rearranging gives us the equation of the locus:
(3x−1)2+(3y)2=a2+b2
Conclusion
The equation of the locus of the centroid of the triangle is:
(3x−1)2+(3y)2=a2+b2
The centroid G of a triangle with vertices (x1,y1), (x2,y2), and (x3,y3) is given by the formula:
G(x,y)=(x1+x2+x33,y1+y2+y33)
For our triangle, the vertices are:
- (x1,y1)=(acosk,asink)
- (x2,y2)=(bsink,−bcosk)
- (x3,y3)=(1,0)
Using the centroid formula:
x=acosk+bsink+13
y=asink−bcosk+03
We can rearrange the equations for x and y:
3x=acosk+bsink+1(1)
3y=asink−bcosk(2)
From equation (1):
acosk+bsink=3x−1(3)
From equation (2):
asink−bcosk=3y(4)
Now, we will square equations (3) and (4) and add them:
(acosk+bsink)2+(asink−bcosk)2=(3x−1)2+(3y)2
a2cos2k+2abcosksink+b2sin2k+a2sin2k−2absinkcosk+b2cos2k=(3x−1)2+(3y)2
Combining the terms gives:
a2(cos2k+sin2k)+b2(sin2k+cos2k)=(3x−1)2+(3y)2
Using the identity cos2k+sin2k=1:
a2+b2=(3x−1)2+(3y)2
Rearranging gives us the equation of the locus:
(3x−1)2+(3y)2=a2+b2
The equation of the locus of the centroid of the triangle is:
(3x−1)2+(3y)2=a2+b2
Similar Questions
Knowledge Check
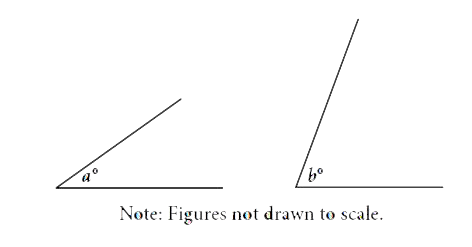
The angles shown above are acute and sin(a∘)=cos(b∘). If a=4k-22 and b= 6k-13, what is the value of k?A4.5B5.5C12.5D21.5
Find the area of the triangle whose vertices are : (acosα,bsinα),(acosβ,bsinβ),(acosγ,bsinγ)
View SolutionThe area of the triangle with vertices (a,0),(acosθ,bsinθ),(acosθ,−bsinθ) is
View SolutionIf the centroid of the triangle formed by the points (3,−5), (−7,4), (10,−k) is at the point (k,−1), then k=
View SolutionThe equation sinx(sinx+cosx)=k has real solutions, where k is a real number. Then
View SolutionThe value of 2sin2θ+kcos22θ=1 , then k is equal to :
View SolutionFor a ΔABC the vertices are A(1,3),B(0,0)andC(k,0). area of △ABC is 3. Find the value of k.
View SolutionThe four lines drawing from the vertices of any tetrahedron to the centroid to the centroid of the opposite faces meet in a point whose distance from each vertex is 'k' times the distance from each vertex to the opposite face, where k is
View Solution

