A circuit having resistor of 2 mega-ohm and capacitor of 1μF is placed in series with a battery of 2 volt. Find the time after which the charge reaches 86.4% of its maximum value.
To solve the problem step by step, we will follow the process of analyzing the charging of a capacitor in an RC circuit.
Step 1: Identify the given values
- Resistance R=2MΩ=2×106Ω
- Capacitance C=1μF=1×10−6F
- Voltage V=2V
Step 2: Calculate the time constant τ
The time constant τ for an RC circuit is given by:
τ=R×C
Substituting the values:
τ=(2×106Ω)×(1×10−6F)=2s
Step 3: Determine the maximum charge Q0
The maximum charge Q0 on the capacitor can be calculated using:
Q0=C×V
Substituting the values:
Q0=(1×10−6F)×(2V)=2×10−6C
Step 4: Calculate the charge at 86.4% of maximum value
We need to find the charge Q when it reaches 86.4% of Q0:
Q=0.864×Q0=0.864×(2×10−6C)=1.728×10−6C
Step 5: Use the charging equation
The charge Q on the capacitor at time t is given by:
Q=Q0(1−e−t/τ)
Substituting the values:
1.728×10−6=2×10−6(1−e−t/2)
Step 6: Solve for e−t/τ
Rearranging the equation gives:
1.728×10−62×10−6=1−e−t/2
0.864=1−e−t/2
e−t/2=1−0.864=0.136
Step 7: Take the natural logarithm
Taking the natural logarithm of both sides:
−t/2=ln(0.136)
t/2=−ln(0.136)
t=−2ln(0.136)
Step 8: Calculate t
Calculating ln(0.136):
ln(0.136)≈−1.993
Thus,
t=−2×(−1.993)≈3.986s
Step 9: Round the answer
Rounding the answer gives:
t≈4s
Final Answer
The time after which the charge reaches 86.4% of its maximum value is approximately 4 seconds.
- Resistance R=2MΩ=2×106Ω
- Capacitance C=1μF=1×10−6F
- Voltage V=2V
The time constant τ for an RC circuit is given by:
τ=R×C
Substituting the values:
τ=(2×106Ω)×(1×10−6F)=2s
The maximum charge Q0 on the capacitor can be calculated using:
Q0=C×V
Substituting the values:
Q0=(1×10−6F)×(2V)=2×10−6C
We need to find the charge Q when it reaches 86.4% of Q0:
Q=0.864×Q0=0.864×(2×10−6C)=1.728×10−6C
The charge Q on the capacitor at time t is given by:
Q=Q0(1−e−t/τ)
Substituting the values:
1.728×10−6=2×10−6(1−e−t/2)
Rearranging the equation gives:
1.728×10−62×10−6=1−e−t/2
0.864=1−e−t/2
e−t/2=1−0.864=0.136
Taking the natural logarithm of both sides:
−t/2=ln(0.136)
t/2=−ln(0.136)
t=−2ln(0.136)
Calculating ln(0.136):
ln(0.136)≈−1.993
Thus,
t=−2×(−1.993)≈3.986s
Rounding the answer gives:
t≈4s
The time after which the charge reaches 86.4% of its maximum value is approximately 4 seconds.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:EXERCISE (LONG ANSWER QUESTIONS)
Explore 12 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:EXERCISE (SHORT ANSWER QUESTIONS)
Explore 12 Videos
- COMMUNICATION SYSTEMS Book:AAKASH SERIESChapter:COMMUNICATION SYSTEMS Exercise:PRACTICE EXERCISE (TV Antenna)
Explore 16 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:EXERCISE - IA
Explore 2 Videos
Similar Questions
Find the time after which current in the circuit becomes 80% of its maximum value
View SolutionA 4μF capacitor, a resistance of 2.5MΩ is in series with 12V battery. Find the time after which the potential difference across the capacitor is 3 times the potential difference across the resistor. [ Given In (2) = 0.693]
View Solution
Knowledge Check
A solenoid has an inductance of 10 henty and a resistance of 2 ohm. It is connected to a 10 volt battery. How long will it take for the magnetic energy to reach 1/4 of its maximum value?
A3.5sB2.5sC5.5sD7.5s
A coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before, the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionA simple LR circuit is connected to a battery at time t=0. The energy stored in the inductor reaches half its maximum value at time
View SolutionA condenser of capacity 1 μ F and a resistance 0.5 mega-ohm are connected in series with a DC supply of 2 V. The time constant of circuit is
View SolutionIf maximum energy is stored in capacitor at t = 0 then find the time after which current in the circuit will be maximum.
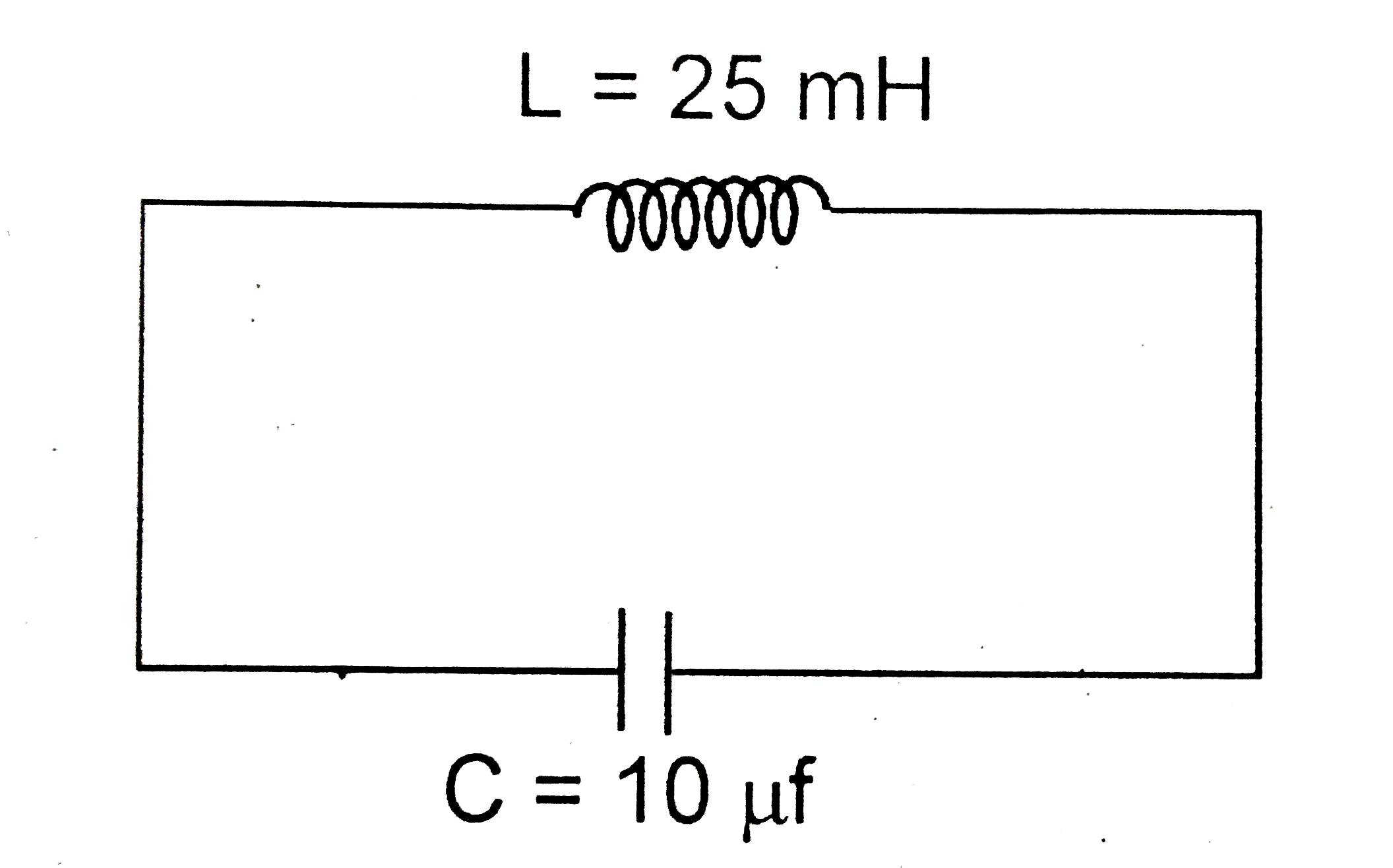
View SolutionAn AC voltage source described by V=10cos(π2)t is connected to a 1μF capacitor as shown in figureure. The key K is closed at t=0. the time (t>0) after which the magntitude of current I reaches its maximum value for the first time is
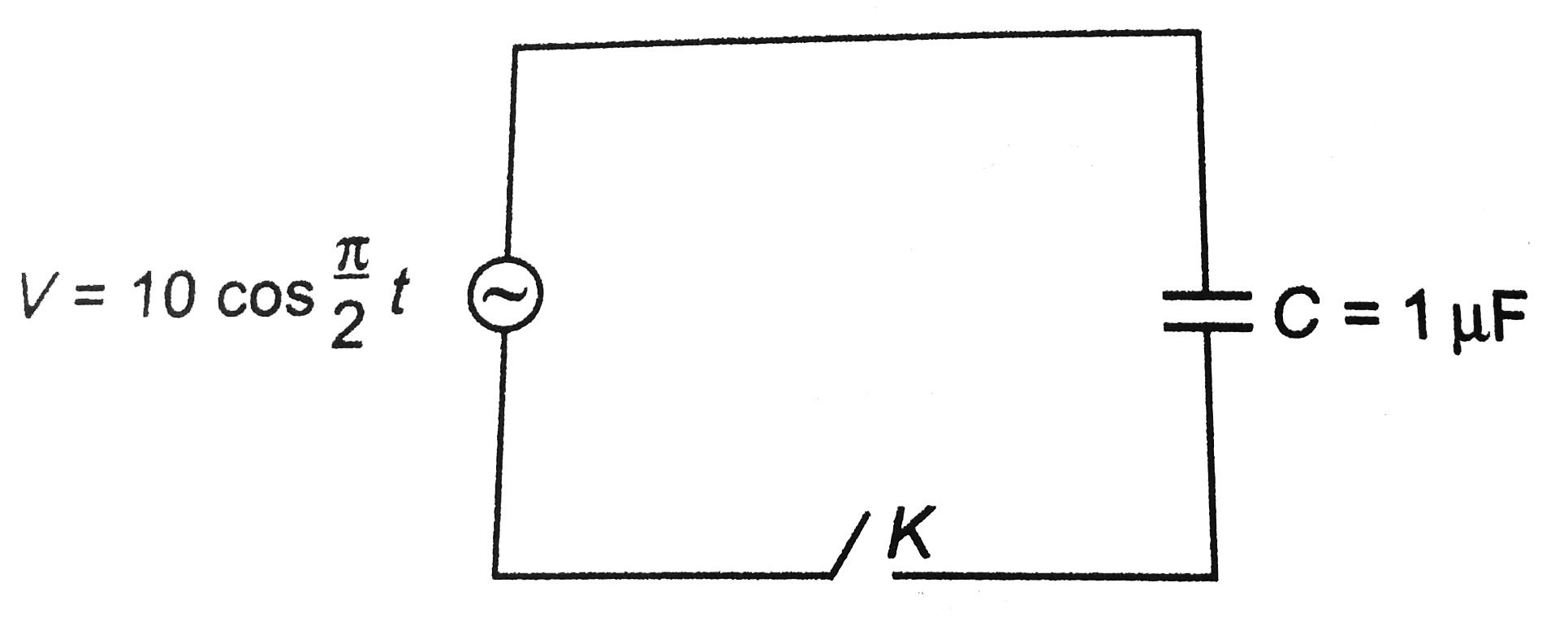 .
.
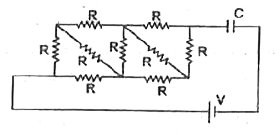
View SolutionIn the circuit shown all the resistors are of same resistance R=11Ω and C=2μF. They are connected through a battery of 10 V. When the cell is switched on, find
(a) maximum current in the circuit, and
(b) energy stored in the capacitor after time t
View SolutionA coil of self-inductance 50 henry is joined to the terminals of a battery of e.m.f. 2 volts through a resistance of 10ohm and a steady current is flowing through the circuit. If the battery is now disconnected, the time in which the current will decay to 1/e of its steady value is
View Solution