In the secondary circuit of a potentiometer , a cell of internal resistance 1.5Ω gives a balancing length of 52 cm. To get a balancing length of 40 cm , how much resistance is to be connected across the cell ?
To solve the problem step by step, we will follow the given information and apply the relevant formulas.
Step 1: Identify the given values
- Internal resistance of the cell, r=1.5Ω
- Balancing length for the first condition, l1=52cm
- Balancing length for the second condition, l2=40cm
Step 2: Understand the relationship between resistance and balancing lengths
In a potentiometer circuit, the relationship between the internal resistance of the cell, the external resistance connected, and the balancing lengths is given by the formula:
r=R×l1−l2l2
where R is the external resistance we need to find.
Step 3: Rearrange the formula to solve for R
Rearranging the formula to isolate R:
R=r×l2l1−l2
Step 4: Substitute the known values into the equation
Substituting the known values into the rearranged formula:
R=1.5×4052−40
Step 5: Simplify the expression
Calculating the denominator:
52−40=12
Now substituting this back into the equation:
R=1.5×4012
Step 6: Perform the multiplication
Calculating 4012:
4012=103≈3.33
Now substituting this back:
R=1.5×3.33≈5Ω
Conclusion
The external resistance R that needs to be connected across the cell to achieve a balancing length of 40 cm is:
5Ω
- Internal resistance of the cell, r=1.5Ω
- Balancing length for the first condition, l1=52cm
- Balancing length for the second condition, l2=40cm
In a potentiometer circuit, the relationship between the internal resistance of the cell, the external resistance connected, and the balancing lengths is given by the formula:
r=R×l1−l2l2
where R is the external resistance we need to find.
Rearranging the formula to isolate R:
R=r×l2l1−l2
Substituting the known values into the rearranged formula:
R=1.5×4052−40
Calculating the denominator:
52−40=12
Now substituting this back into the equation:
R=1.5×4012
Calculating 4012:
4012=103≈3.33
Now substituting this back:
R=1.5×3.33≈5Ω
The external resistance R that needs to be connected across the cell to achieve a balancing length of 40 cm is:
5Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
12 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
12 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
Similar Questions
When a Daniel cell is connected in the secondary circuit of a potentiometer, the balancing length is found to be 540 cm. If the balancing length becomes 500 cm. When the cell is short-circuited with 1Ω, the internal resistance of the cell is
View SolutionThe emf of the driver cell of a potentiometer is 2V, and its internal resistance is negligible. The length of the potentiometer wire is 100cm, and resistance is 5ohm. How much resistance is to be connected in series with the potentiometer wire to have a potential gradient of 0.05mVcm−1?
View SolutionIn potentiometer experiment, a cell of emf 1.25V gives balancing length of 30 cm. If the cell is replaced by another cell, then balancing length is found to be 40 cm. What is the emf of second cell ?
View SolutionFor the given circuit,
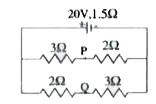
If internal resistance of cell is 1.5Ω, then
View SolutionThe length of the potentiometer wire is 600 cm and a current of 40 mA is flowing in it. When a cell of emf 2 V and internal resistance 10Ω is balanced on this potentiometer the balance length is found to be 500 cm. The resistance of potentiometer wire will be
View SolutionIn an experiment with a potentiometer, the null point is
obtained at a distance of 60cm along the wire from the
common terminal with a leclanche cell. When a shunt
resistance of 1Ω is connected across the cell, the null
point shifts to a distance of 30cm from the common
terminal. what is the internal resistance of the cell?
View SolutionA battery of unknown emf connected to a potentiometer has balancing length 560 cm. If a resistor of resistance 10 ohm, is connected in parallel with the cell the balancing length change by 60 cm. If the internal resistance of the cell is n10 ohm, the value of 'n' is
View Solutionis made of uniform material and cross-sectional area, and it has uniform resistance per unit length. The potential gradient depends upon the current in the wire.
A potentiometer with a cell of emf 2V and internal resistance 0.4Ω is used across the wire AB. A standard cadmium cell of emf 1.02V gives a balance point at 66cm length of wire. The standard cell is then replaced by a cell of unknows emf e (internal resistance r), and the balance. Point found similarly turns out to be 88cm length of the wire. The length of potentiometer wire AB is 1m.
The reading of the potentiometer, if a 4V battery is used instead of e is
View SolutionIn a potentiometer arrangement, a cell of emf 1.5 V gives a balance point at 27 cm length of wire. If the cell is replaced by another cell and balance point shifts to 54 cm, the emf of the second cell is :
View SolutionWhen 6 identical cells of no internal resistance are connected in series in the secondarycircuit of a potentio meter, the balancing lengths is .l., balancing length becomes 1/3 when some cells are connected wrongly, the number of cells connected wrongly are
View Solution
