When a battery is connected to the resistance of 10Ω the current in the circuit is 0.12 A . The same battery gives 0.07A current with 20Ω Calculate e.m.f and internal resistance of the battery.
To solve the problem of finding the e.m.f (electromotive force) and internal resistance of the battery, we can follow these steps:
Step 1: Set Up the Equations
We know from Ohm's law that the e.m.f (E) of the battery can be expressed in terms of the current (I), external resistance (R), and internal resistance (r) as follows:
E=I⋅R+I⋅r
This can be rearranged to:
E=I(R+r)
Step 2: Apply the First Case
For the first case where the external resistance R1=10Ω and the current I1=0.12A:
E=0.12⋅10+0.12⋅r
This simplifies to:
E=1.2+0.12r
Let’s label this as Equation (1).
Step 3: Apply the Second Case
For the second case where the external resistance R2=20Ω and the current I2=0.07A:
E=0.07⋅20+0.07⋅r
This simplifies to:
E=1.4+0.07r
Let’s label this as Equation (2).
Step 4: Set the Two Equations Equal
Since both equations equal E, we can set them equal to each other:
1.2+0.12r=1.4+0.07r
Step 5: Solve for Internal Resistance (r)
Rearranging the equation gives:
0.12r−0.07r=1.4−1.2
This simplifies to:
0.05r=0.2
Now, divide both sides by 0.05:
r=0.20.05=4Ω
Step 6: Substitute r Back to Find E
Now that we have the internal resistance r=4Ω, we can substitute this value back into either Equation (1) or Equation (2) to find the e.m.f (E). Using Equation (1):
E=1.2+0.12⋅4
Calculating this gives:
E=1.2+0.48=1.68V
Final Results
Thus, the e.m.f of the battery is E=1.68V and the internal resistance is r=4Ω.
---
We know from Ohm's law that the e.m.f (E) of the battery can be expressed in terms of the current (I), external resistance (R), and internal resistance (r) as follows:
E=I⋅R+I⋅r
This can be rearranged to:
E=I(R+r)
For the first case where the external resistance R1=10Ω and the current I1=0.12A:
E=0.12⋅10+0.12⋅r
This simplifies to:
E=1.2+0.12r
Let’s label this as Equation (1).
For the second case where the external resistance R2=20Ω and the current I2=0.07A:
E=0.07⋅20+0.07⋅r
This simplifies to:
E=1.4+0.07r
Let’s label this as Equation (2).
Since both equations equal E, we can set them equal to each other:
1.2+0.12r=1.4+0.07r
Rearranging the equation gives:
0.12r−0.07r=1.4−1.2
This simplifies to:
0.05r=0.2
Now, divide both sides by 0.05:
r=0.20.05=4Ω
Now that we have the internal resistance r=4Ω, we can substitute this value back into either Equation (1) or Equation (2) to find the e.m.f (E). Using Equation (1):
E=1.2+0.12⋅4
Calculating this gives:
E=1.2+0.48=1.68V
Thus, the e.m.f of the battery is E=1.68V and the internal resistance is r=4Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
12 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
12 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
Similar Questions
the current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View Solution
Knowledge Check
A battery of emf 15 V and internal resistance of 4Ω is connected to a resistor. If the current in the circuit is 2A and the circuit is closed. Resistance of the resistor and terminal voltage of the battery will be
A2.5Ω,6VB3.5Ω,6VC2.5Ω,7VD3.5Ω,7V
When a battery connected across a resistor of 16Ω, the voltage across the resistor is 12 V. When the same battery is connected across a resistor of 10Ω, voltage across it is 11 V. The internal resistance of the battery (in ohm) is
View SolutionA cell supplies a current of 2 A when it is connected to a 5Ω resistance and supplies a current of 1.2 A, if it is connected to a resistance of 9 Ω. Find the e.m.f and internal resistance of the cell.
View SolutionIn fig. battery E is balanced on 55cm length of potentiometer wire but when a resistance of 10Ω is connected in parallel with the battery then it balances on 50cm length of the potentiometer wire then internal resistance r of the battery is:-
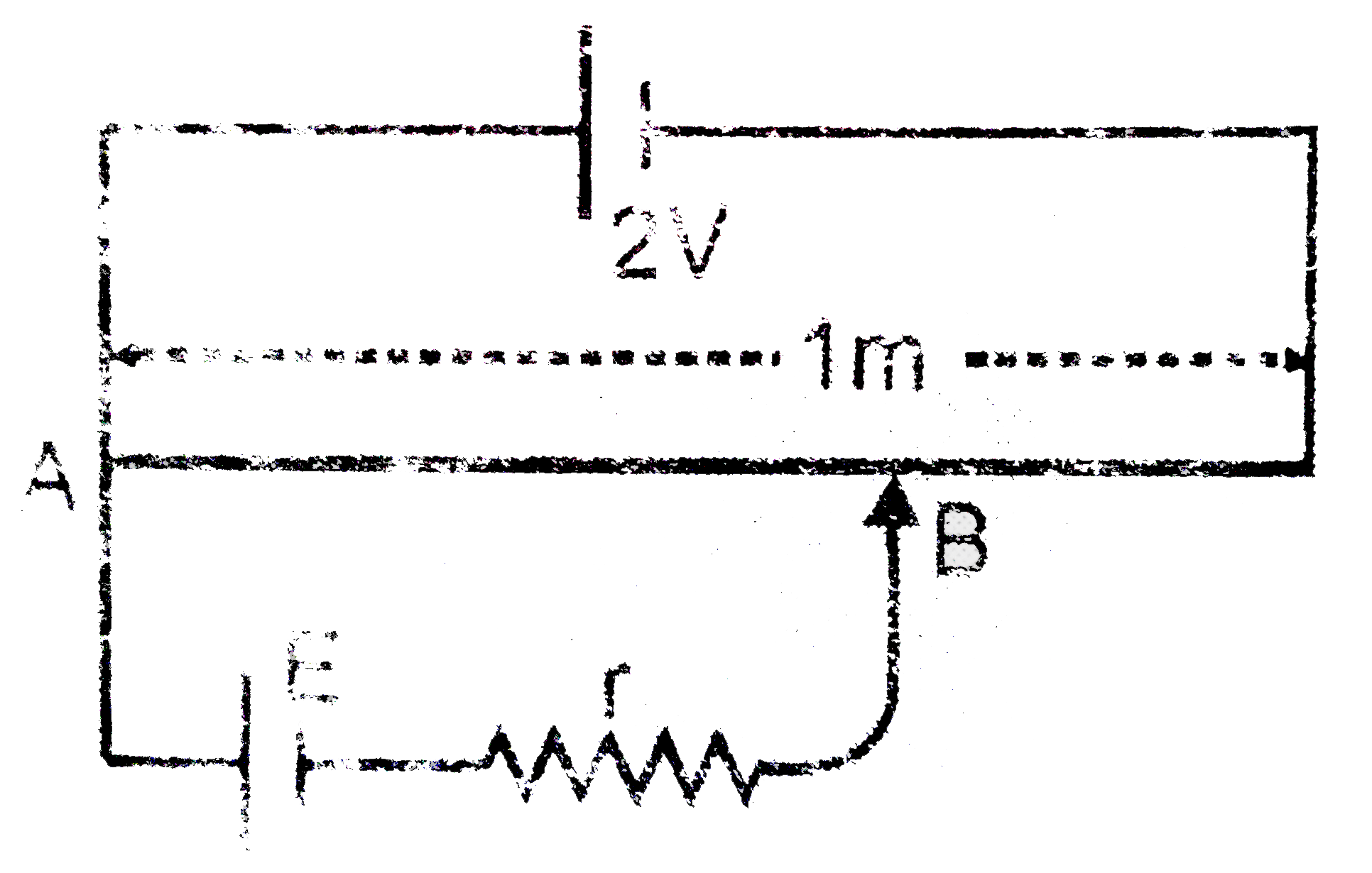
View SolutionA galvanometer, together with an unknown resistance in series, is connected across two identical batteries of each 1.5V. When the batteries are connected in series,the galvanometer records a current of 1A, and when the batteries are connected in parallel, the current is 0.6A. In this case, the internal resistance of the battery is
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistors ? What is the terminal voltage of the battery when the circuit is closed ?
View SolutionA battery of e.m.f 3 V supplies current through a circuit in which the resistance can be changed. A high resistance voltmeter is connected across the battery. When the current is 1.5 A, the voltmeter reads 2.7 V. Find the internal resistance of the battery.
View SolutionA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View Solution
