The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law
R=R0[1+a(T−T0)]
The resistance is 101.6Ω at the triple-point of water 273.16 K, and 165.5Ω at the normal melting point of lead (600.5 K). What is the temperature when the resistance is 123.4Ω?
Here, R0=101.6Ω,T0=273.16 K
Case (i) R1=165.5Ω,T1=600.5K
Case (ii) R2=123.4Ω,T2=?
Using the relation R = R0[1+α(T−T0)]
Case (i) 165.5=101.6[1+α(600.5−273.16)]
α=165.5−101.6101.6×(600.5−273.16)=63.9101.6×372.34
Case (ii) 123.4 = 101.6[1+α(T2−273.16)]
or 123.4=101.6[1+63.9101.6×327.34(T2−273.16)]
= 101.6 + 63.9327.34(T2−273.16)
or T2(124.4−101.6)×327.3463.9+273.16
= 111.67 + 273.16 = 384.83K
Similar Questions
The electrical resistance in ohms of a certain thermometer varies with temperature ac cording to the approximate law: R=R0[1+α(T−T0)]
The resistances is 101.6Ω at the triple-point of water 273.16K, and 165.5Ω at the normal melting point of lead (600.5K). What is the temperature when the resistance is 123.4Ω?
View SolutionThe resistance R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
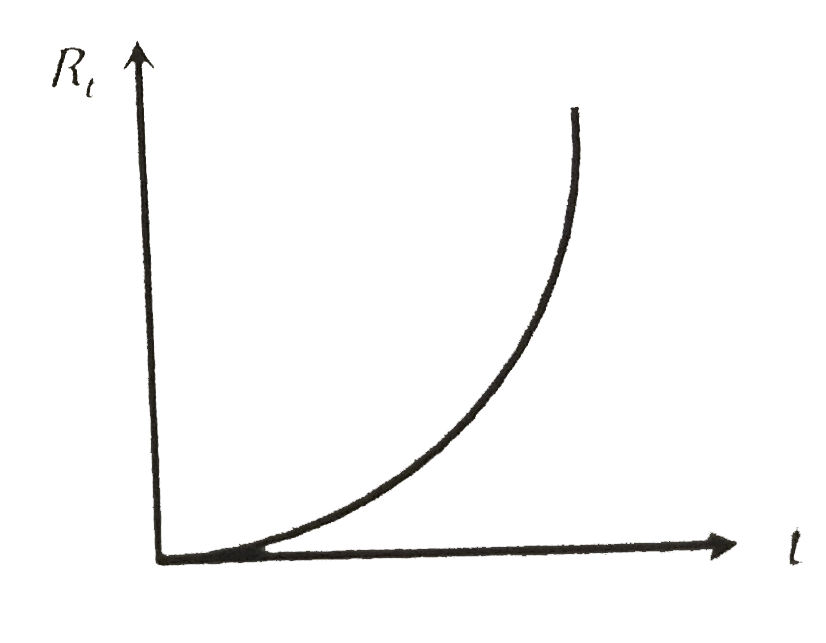
View Solution
Knowledge Check
The magnetic flux (ϕ) in a closed circuit of resistance 20Ω varies with time (t) according to the equation ϕ=7t2−4t where ϕ is in weber and t is in seconds. The magnitude of the induced current at t =0.25s is
A25mAB0.025mAC47 mAD175 mA
The temperature coefficient of resistance of a wire is 0.00125 per ∘C. At 300 K, its resistance is 1Ω. The resistance of the wire will be 2Ω at
View SolutionThe resistance of a platinum wire of platinum resistance thermometer at the ice point is 5Ω and at steam point is 5.23Ω. When therometer is insertes in a hot bath, the resistance of the platinum wire is 5.795Ω. Calculate the temperature of the bath?
View SolutionThe network shown in figure is an arrangement of nine identical resistors. The resistance of the network between points A and B is 1.5Ω. The resistance r is
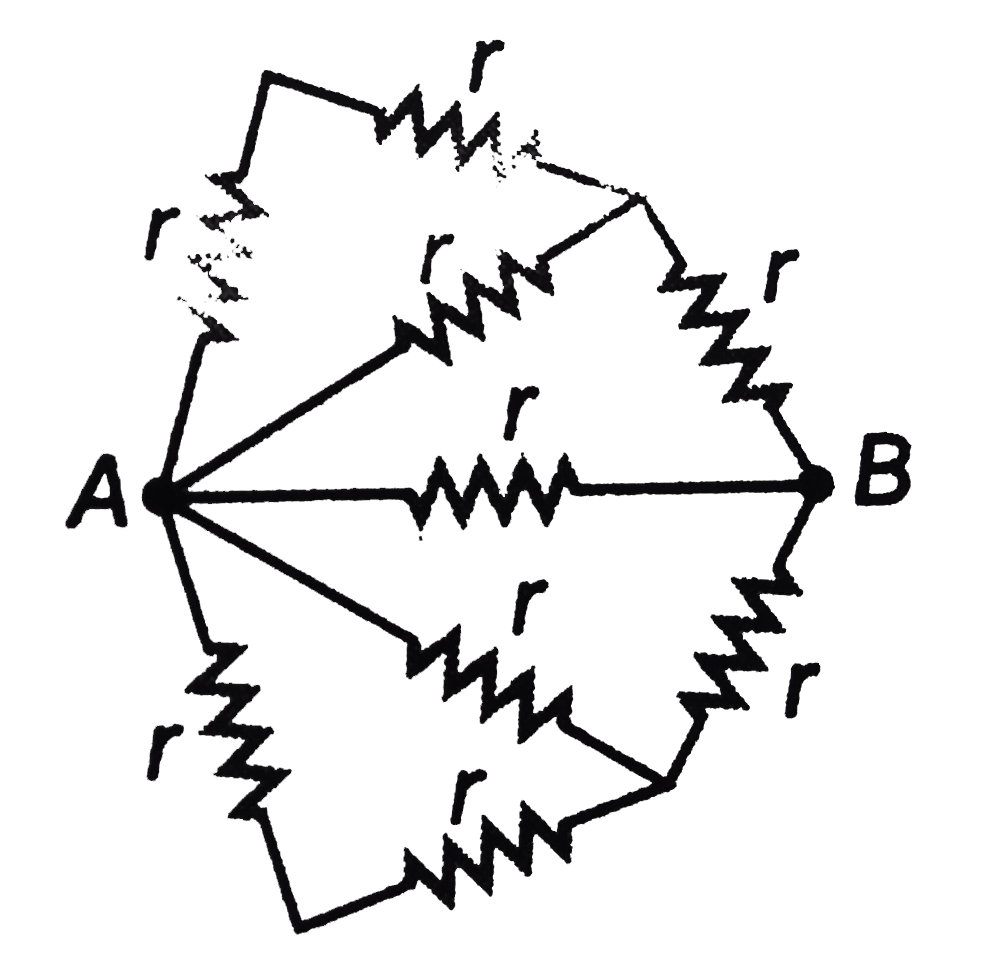
View SolutionA resistance thermometer measures temperature with the increase in resistance of a wire of high temperature. If the wire is platinum and has resistance of 10Ω at 20∘C and a resistance of 35Ω in a hot furnace, what is the temperature of the hot furnace? (αplatinum=0.0036∘C−1)
View SolutionAt room temperature (27.0∘C) the resistance of a heating element is 100Ω. What is the temperature of the element if the resistance is found to be 117Ω, given that the temperature coefficient of the material of the resistor is (1.70×10−4)∘C−1.
View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.
View SolutionThe electrical resistance of pure platinum increases linearly with increasing temperature over a small range of temperature . This property is used in a Platinum resistance thermometer. The relation between Rθ (Resistance at θ K) and R0 (Resistance at θ0K) is given by Rθ=R0[1+a(θ−θ0)], where α= temperature coefficient of resistance. Now, if a Platinum resistance thermometer reads 0∘C when its resistance is 80Ω and 100∘C when its resistance is 90Ω find the temperature at which its resistance is 86Ω.
View Solution
