A bar magnet of magnetic moment 10Am2 has a cross sectional area of 2.5×10−4m2. If the intensity of magnetisation of the magnet is 106Am−1, find the length of the magnet?
To find the length of the bar magnet given the magnetic moment, cross-sectional area, and intensity of magnetization, we can follow these steps:
1. Identify the Given Values:
- Magnetic Moment (M) = 10 A·m²
- Cross-sectional Area (A) = 2.5 × 10^(-4) m²
- Intensity of Magnetization (I) = 10^6 A/m
2. Use the Formula for Magnetic Moment:
The magnetic moment (M) of a bar magnet can be expressed as:
M=I×A×L
where:
- L is the length of the magnet.
3. Rearranging the Formula:
To find the length L, we rearrange the formula:
L=MI×A
4. Substituting the Values:
Now, we substitute the given values into the formula:
L=10(106)×(2.5×10−4)
5. Calculating the Denominator:
Calculate the denominator:
I×A=106×2.5×10−4=2.5×102=250
6. Calculating the Length:
Now, substitute this back into the equation for L:
L=10250=0.04 m
7. Finding the Actual Length of the Magnet:
Since the total length of the bar magnet is 2L:
2L=0.04 m
Therefore, the length of the magnet L is:
L=0.042=0.02 m
Final Answer:
The length of the magnet is 0.02 m or 2 cm.
- Magnetic Moment (M) = 10 A·m²
- Cross-sectional Area (A) = 2.5 × 10^(-4) m²
- Intensity of Magnetization (I) = 10^6 A/m
The magnetic moment (M) of a bar magnet can be expressed as:
M=I×A×L
where:
- L is the length of the magnet.
To find the length L, we rearrange the formula:
L=MI×A
Now, we substitute the given values into the formula:
L=10(106)×(2.5×10−4)
Calculate the denominator:
I×A=106×2.5×10−4=2.5×102=250
Now, substitute this back into the equation for L:
L=10250=0.04 m
Since the total length of the bar magnet is 2L:
2L=0.04 m
Therefore, the length of the magnet L is:
L=0.042=0.02 m
The length of the magnet is 0.02 m or 2 cm.
Topper's Solved these Questions
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - PROBLEMS (LEVEL-II)
16 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS)
25 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
Similar Questions
A bar mangnet has length 3 cm cross sectional area 2 cm2 and magnetic moment 3 Am2 the intensity of magnetisation of the bar magnet is
View SolutionA bar magnet of magnetic moment 3.0A−m2 is placed in a uniform magnetic induction field of 2×10−5T. If each pole of the magnet experiences a force of 6×10−4N, the length of the magnet is
View SolutionA bar magnet made of steel has a magnetic moment of 2.5Am2 and amass of 6.6×10−5kg. If the density of steel is 7.9×103kgm−3, find the intensity of magnetization of the magnet.
View SolutionA magnet of magnetic moment 10 Am2 has magnetic length 5 cm.The strength of magnet is
View SolutionA bar magnet of magnetic dipole moment 8 Am2 has poles separated by 0.4 m . Find the pole strength of bar magnet .
View SolutionA paramagnetic substance of susceptibility 3×10−4 is placed in a magnetic field of 3×10−4Am−1. . Then , the intensity of magnetisation in units of A m−1 is
View SolutionTwo short magnets of magnetic moment 1000Am2 are placed as shown at the corners of a square of side 10cm. The net magnetic induction at P is
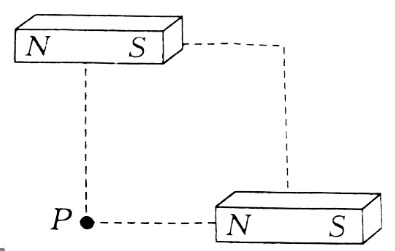
View SolutionTwo magnets of magnetic moments 4Am2and3Am2 are joined to form a cross (+), then the magnetic moment of the combination is
View SolutionThe work done in rotating a magent of the magnetic moment 2Am2 in a magnetic field of induction 5×10−3T from the direction along the magnetic field to the direction opposite to the field , is
View SolutionA straight solenoid of length 50 cm has 1000 turns per metre and mean cross-sectional area of 2×10−4m2 . It is placed with its axis of 30∘ with uniform magnetic field of 0.32 T . Find the torque acting on the solenoid when a current of 2 ampere is passed through it .
View Solution
