Two simple harmonic motions $y_{1} = A sin ω t$ and $y_{2}$ = Acos $ω$ t are superimposed on a particle of mass m. The total mechanical energy of the particle is

Video Solution

Text Solution

Verified by Experts

Phase difference between the two SHMs is $90^{\circ}$
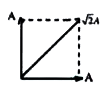
Therefore, resultant amplitude is
$A = \sqrt{2 A}, E = \frac{1}{2} m ω^{2} A_{R}^{2} = \frac{1}{2} m ω^{2} {(\sqrt{2} A)}^{2} - m ω^{2} A^{2}$

Updated on:21/07/2023

|

Class 11 PHYSICS OSCILLATION

Similar Questions

Two waves of equation
$y_{1} = a cos (ω t + k x) and y_{2} = a cos (ω t - k x)$ are superimposed upon each other. They will produce
View Solution
When two displacement represented by $y_{1} = a sin (ω t)$ and $y_{2} = b cos (ω t)$ are superimposed, the motion is
View Solution
Two simple harmonic motions given by, $x = a sin (ω t + δ)$ and $y = a sin (ω t + δ + \frac{π}{2})$ act on a particle will be
View Solution
Two SHMs directed along x-axis and y-axis are superimposed on a particle of mass m. If $x = A_{1} sin ω t$ and y= A_2 sin(omegat+pi),then path of the particle will be.
View Solution
Two SHMs $s_{1} = a sin ω t$ and $s_{2} = b sin ω t$ are superimposed on a particle. The $s_{1}$ and $s_{2}$ are along the direction which makes $37^{\circ}$ to each other
View Solution
Passage I) In simple harmonic motion force acting on a particle is given as $F = - 4 x$ , total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is $- 16 \frac{m}{s^{2}}$ . Mass of the particle is 0.5 kg.
At x=+1m, potential energy and kinetic energy of the particle are
View Solution
Passage I) In simple harmonic motion force acting on a particle is given as $F = - 4 x$ , total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is $- 16 \frac{m}{s^{2}}$ . Mass of the particle is 0.5 kg.
Potential energy of the particle at mean position is
View Solution
Passage I) In simple harmonic motion force acting on a particle is given as $F = - 4 x$ , total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is $- 16 \frac{m}{s^{2}}$ . Mass of the particle is 0.5 kg.
Displacement time equation equation of the particle is
View Solution
A particle is subjected to two simple harmonic motions.
$x_{1} = 4.0 sin (100 π t)$ and $x_{2} = 3.0 sin (100 π t + \frac{π}{3})$
Find
(a) the displacement at $t = 0$
(b) the maximum speed of the particle and
(c ) the maximum acceleration of the particle.
View Solution
The particle executing simple harmonic motion has a kinetic energy $K_{0} {cos}^{2} ω t$ . The maximum values of the potential energy and the energy are respectively
View Solution

Recommended Questions

Home
Ask Doubt
Profile