Simplify using Boolean Algebra. Draw the resultant simplified logic circuit.
To simplify the expression Y=AB+ABC+¯¯¯¯AB+A¯¯¯¯BC using Boolean algebra, we can follow these steps:
Step 1: Write the original expression
Start with the original expression:
Y=AB+ABC+¯¯¯¯AB+A¯¯¯¯BC
Step 2: Rearrange the terms
Rearranging the terms gives:
Y=AB+ABC+¯¯¯¯AB+A¯¯¯¯BC
Step 3: Factor out common terms
Notice that AB and ABC share a common factor of AB:
Y=AB(1+C)+¯¯¯¯AB+A¯¯¯¯BC
Since 1+C=1, we can simplify this to:
Y=AB+¯¯¯¯AB+A¯¯¯¯BC
Step 4: Combine terms
Now, we can combine AB and ¯¯¯¯AB:
Y=B(A+¯¯¯¯A)+A¯¯¯¯BC
Since A+¯¯¯¯A=1:
Y=B+A¯¯¯¯BC
Step 5: Final simplification
Now we need to check if we can simplify A¯¯¯¯BC further. However, since it does not share common factors with B, we leave it as is:
Y=B+A¯¯¯¯BC
Result
The simplified expression is:
Y=B+A¯¯¯¯BC
Step 6: Draw the logic circuit
To draw the logic circuit for the simplified expression Y=B+A¯¯¯¯BC:
1. Inputs: A, B, C
2. NOT gate: To get ¯¯¯¯B from B.
3. AND gate: To combine A and ¯¯¯¯B and C to get A¯¯¯¯BC.
4. OR gate: To combine B and A¯¯¯¯BC to get the output Y.
Start with the original expression:
Y=AB+ABC+¯¯¯¯AB+A¯¯¯¯BC
Rearranging the terms gives:
Y=AB+ABC+¯¯¯¯AB+A¯¯¯¯BC
Notice that AB and ABC share a common factor of AB:
Y=AB(1+C)+¯¯¯¯AB+A¯¯¯¯BC
Since 1+C=1, we can simplify this to:
Y=AB+¯¯¯¯AB+A¯¯¯¯BC
Now, we can combine AB and ¯¯¯¯AB:
Y=B(A+¯¯¯¯A)+A¯¯¯¯BC
Since A+¯¯¯¯A=1:
Y=B+A¯¯¯¯BC
Now we need to check if we can simplify A¯¯¯¯BC further. However, since it does not share common factors with B, we leave it as is:
Y=B+A¯¯¯¯BC
The simplified expression is:
Y=B+A¯¯¯¯BC
To draw the logic circuit for the simplified expression Y=B+A¯¯¯¯BC:
2. NOT gate: To get ¯¯¯¯B from B.
3. AND gate: To combine A and ¯¯¯¯B and C to get A¯¯¯¯BC.
4. OR gate: To combine B and A¯¯¯¯BC to get the output Y.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE -I (ENERGY BANDS AND CLASSIFICATION OF SOLIDS )41videos
SEMICONDUCTOR DEVICES
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE -I (P-N JUNCTION DIODE)30videos
SEMICONDUCTOR DEVICES
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - Problems (LEVEL-II)9videos
SEMICONDUCTOR DEVICES
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)60videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE45videos
UNITS AND MEASUREMENT
Similar Questions
A, B and C represent switches in 'on' position and A', B' and C' represent them in 'off' position. Construct a switching circuit representing the polynomial ABC + AB'C + A'B'C. Using Boolean Algebra, prove that the given polynomial can be simplified to C (A + B'). Construct an equivalent switching circuit.
View SolutionConstruct a circuit diagram for the following Boolean Function
(BC+A)(A'B'+C')+A'B'C'
Using laws of Boolean Algebra, simplify the function and draw the simplified circuit.View SolutionP,Q and R represent switches in on position and P',Q' and R' represent switches in off position. Construct a switching circuit representing the polynomial PR+Q(Q'+R)(P÷QR) . Using Boolean Algebra, simplify the polynomial expression and construct the simplified circuit
View SolutionIf A,B and C are the elements of Boolean algebra, simplify the expression (A'+B') (A+C')+B' (B+C). Draw the simplified circuit.
View SolutionWrite the Boolean function coresponding to the switching circuit given below:

A, B and C represent switches in 'on' position and A', B' and C' represent them in 'off' position. Using Boolean algebra, simplify the function and construct an equivalent switching circuit.View SolutionUsing the wave forms of the input A and B, draw the output waveform of the given logic circuit . Identify the logic gate obtained . Write also the truth table.
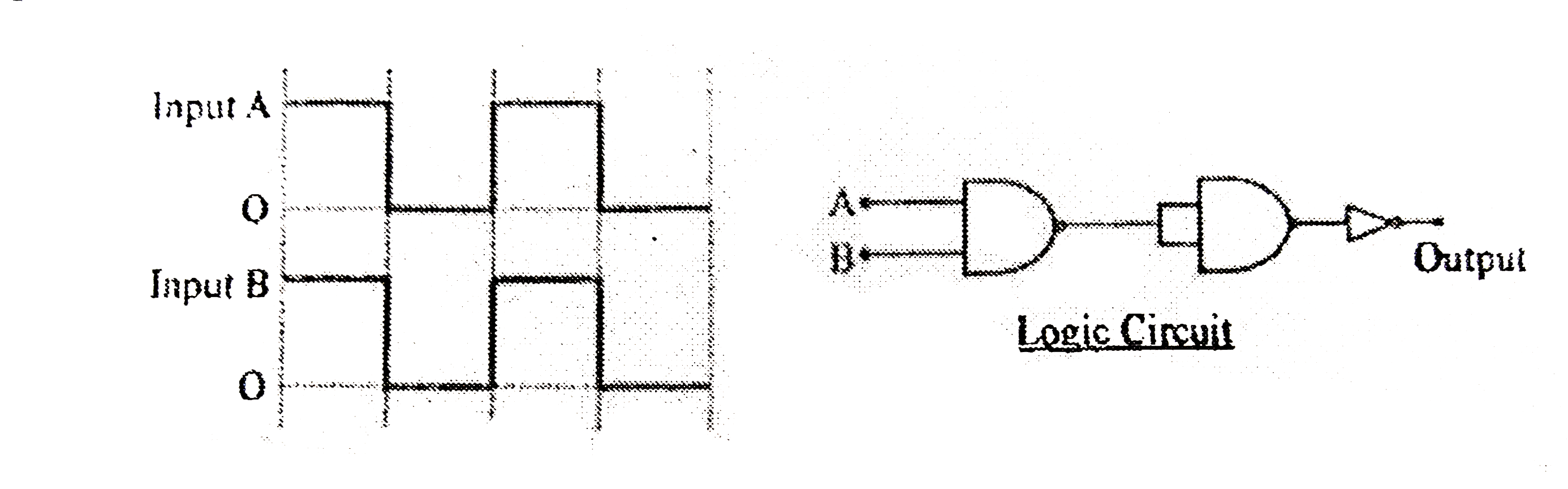 View Solution
View SolutionIt is required to design a (two -input) logic gate, using an appropriate number, of :
(a) NAND gates that gives a 'low' output only when both the inputs are 'low'.
(b) NOR gates that gives a 'high' output only when both the inputs are 'high'.
Draw the logic circuits for these two cases and write the truth table, corresponding to each of the two designs.View SolutionThe method of electrical images is used to solve the electrostatic problems, where charge distribution is not specified completely. The method consists of replacement of given charge distribution by a simplified charge distribution or a signal point charge or a number of point charges [rovided the original boundary conditions are still satisfied. For example consider a system consider a system containing a point charge q placed at a distance d of form an infinite conducting plane. The boundary conditions are :
(i) Potential is zero at infinity (ii) Potential is zero at each point on the conducting plane If we replaced the conducting plane by a point charge (-q) placed at a distance 'd' opposite to conducting plane. The charge (-q) is called the electrical image.
Now system consists of two charge +q an -q at seperation2d. If charge +q moves to a distance 'y' from the boundary of conducting plane (now absent), the electrical image -q also moves to the same 'y' from the boundary of conducting plane, so that the new distance between +q and -q is 2y

The work done in carrying charge q from distance d to distance y from earthed conducting plane isView SolutionThe method of electrical images is used to solve the electrostatic problems, where charge distribution is not specified completely. The method consists of replacement of given charge distribution by a simplified charge distribution or a signal point charge or a number of point charges [rovided the original boundary conditions are still satisfied. For example consider a system consider a system containing a point charge q placed at a distance d of form an infinite conducting plane. The boundary conditions are :
(i) Potential is zero at infinity (ii) Potential is zero at each point on the conducting plane If we replaced the conducting plane by a point charge (-q) placed at a distance 'd' opposite to conducting plane. The charge (-q) is called the electrical image.
Now system consists of two charge +q an -q at seperation2d. If charge +q moves to a distance 'y' from the boundary of conducting plane (now absent), the electrical image -q also moves to the same 'y' from the boundary of conducting plane, so that the new distance between +q and -q is 2y

The force between point charge +q and earthed conducting plane isView SolutionDraw the output waveformed at X, using the given inputs A and B for the logic circuit shows below. Also, identify the logic operation performed by this circuit.
 View Solution
View Solution
