A full wave rectifier uses two diodes with a load resistance of 100Ω. Each diode is having negligible forward resistance. Find the efficiency of this full wave rectifier
To find the efficiency of a full wave rectifier using two diodes with a load resistance of 100Ω and negligible forward resistance, we can follow these steps:
1. Identify the Given Values:
- Load Resistance (RL) = 100Ω
- Forward Resistance of Diodes (RF1 and RF2) = negligible (assumed to be 0Ω)
2. Understand the Efficiency Formula:
- The efficiency (E) of a full wave rectifier can be calculated using the formula:
E=0.812×RLRL+RF1+RF2
3. Substitute the Values into the Formula:
- Since both RF1 and RF2 are negligible, we can substitute RF1=0 and RF2=0 into the formula:
E=0.812×100100+0+0
4. Calculate the Efficiency:
- Simplifying the equation:
E=0.812×100100=0.812
5. Convert Efficiency to Percentage:
- To express the efficiency as a percentage:
Percentage Efficiency=E×100=0.812×100=81.2%
Final Result:
The efficiency of the full wave rectifier is 81.2%.
- Load Resistance (RL) = 100Ω
- Forward Resistance of Diodes (RF1 and RF2) = negligible (assumed to be 0Ω)
- The efficiency (E) of a full wave rectifier can be calculated using the formula:
E=0.812×RLRL+RF1+RF2
- Since both RF1 and RF2 are negligible, we can substitute RF1=0 and RF2=0 into the formula:
E=0.812×100100+0+0
- Simplifying the equation:
E=0.812×100100=0.812
- To express the efficiency as a percentage:
Percentage Efficiency=E×100=0.812×100=81.2%
The efficiency of the full wave rectifier is 81.2%.
Topper's Solved these Questions
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE -I (ENERGY BANDS AND CLASSIFICATION OF SOLIDS )
41 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE -I (P-N JUNCTION DIODE)
30 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - Problems (LEVEL-II)
9 Videos
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)
60 Videos
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE
45 Videos
Similar Questions
Knowledge Check
The circuit shown in the figure contains two diodes each with a forward resistance of 30 Ω and with infinite backward resistance. If the battery is 3 V, the current through the 50 Ω resistance (in ampere) is
 AzeroB0.01C0.02D0.03
AzeroB0.01C0.02D0.03The potentiometer wire of length 200cm has a resistance of 20Ω. It is connected in series with a resistance 10Ω and an accumulator of emf 6V having negligible internal resistance. A source of 2.4V is balanced against length 1 of the potentiometer wire. Find the length l of the potentiometer wire. Find the length l
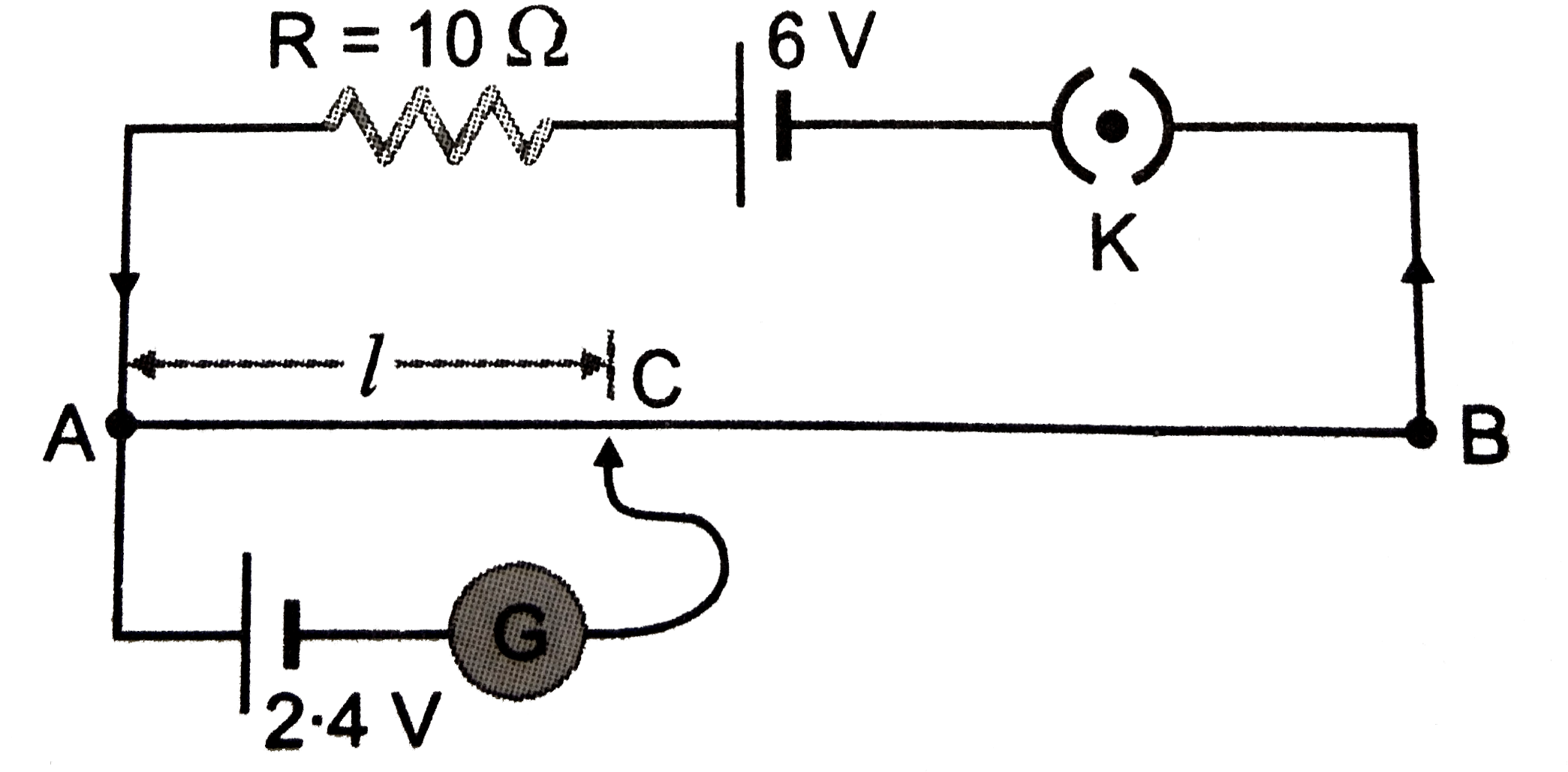 A100cmB120cmC110cmD140cm
A100cmB120cmC110cmD140cm
What is the output form of full-wave rectifier ?
View SolutionThe circuit shown in the figure contains two diodes each with a forward resistance of 50Ω and with infinite backward resistance. If the batter of 6 V is connected in the circuit, then the current through the 100Ω resistance is
View SolutionIn input in a full - wave rectifier is e=50sin(314t) volt, diode resistance is 100Ω and load resistance is 1kΩ then, pulse frequency of output voltage is
View SolutionA sinusoidal voltage of amplitude 25 volts and frequency 50 Hz is applied to a half wave rectifier using PN diode. No filter is used and the load resistor is 1000Ω. The forward resistance Rf ideal diode is 10Ω. Calculate.
(i) Peak, average and rms values of load current
(ii) d.c power output
(ii) a.c power input
(iv) % Rectifier efficiency
(v) Ripple factor.
View SolutionThe circuit shown in figure (1) Contains two diodes each with a forward resistance of 50ohm and with infinite reverse resistance. If the battery voltage is 6V, the current through the 100ohm resistance is.
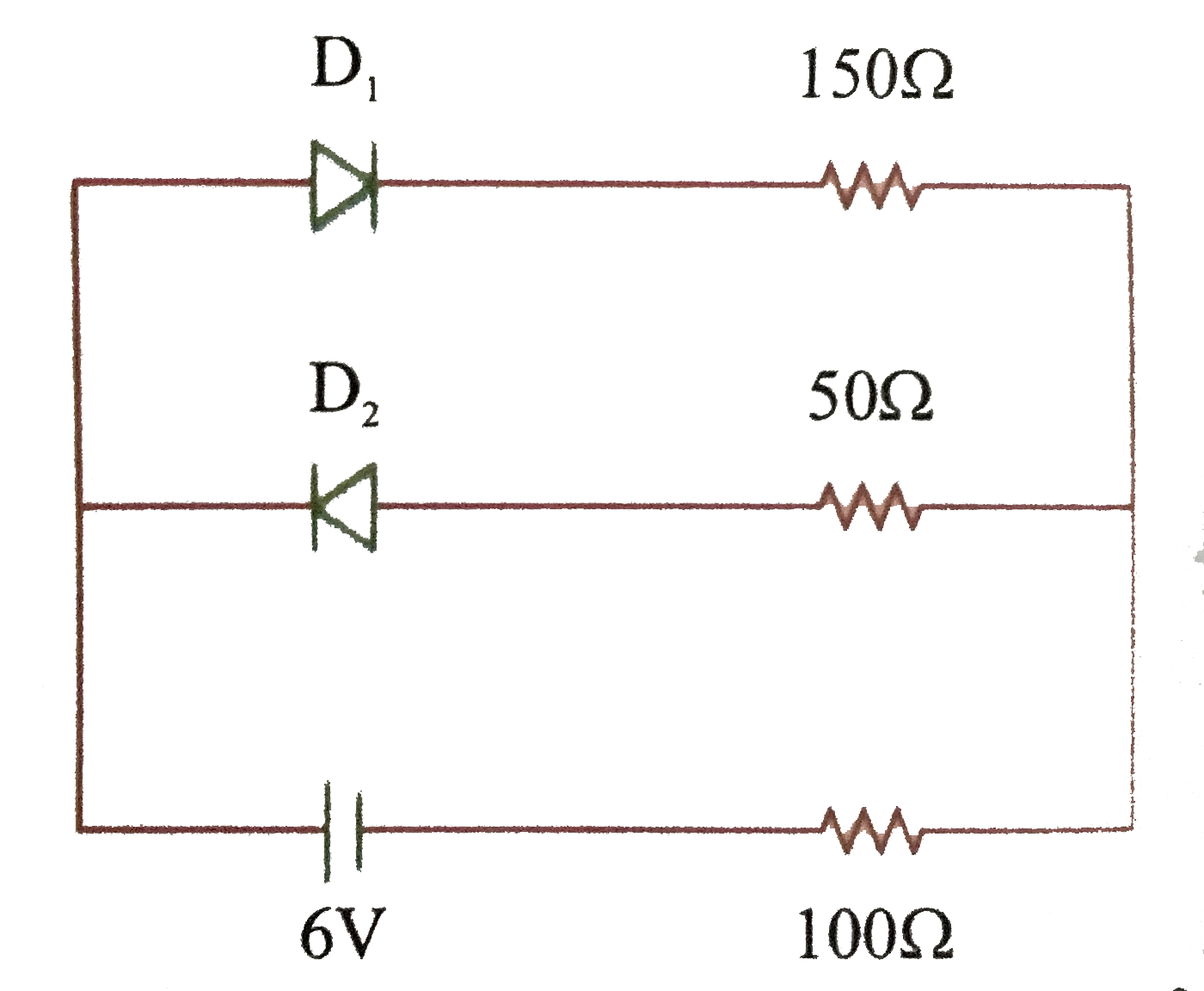 .
.
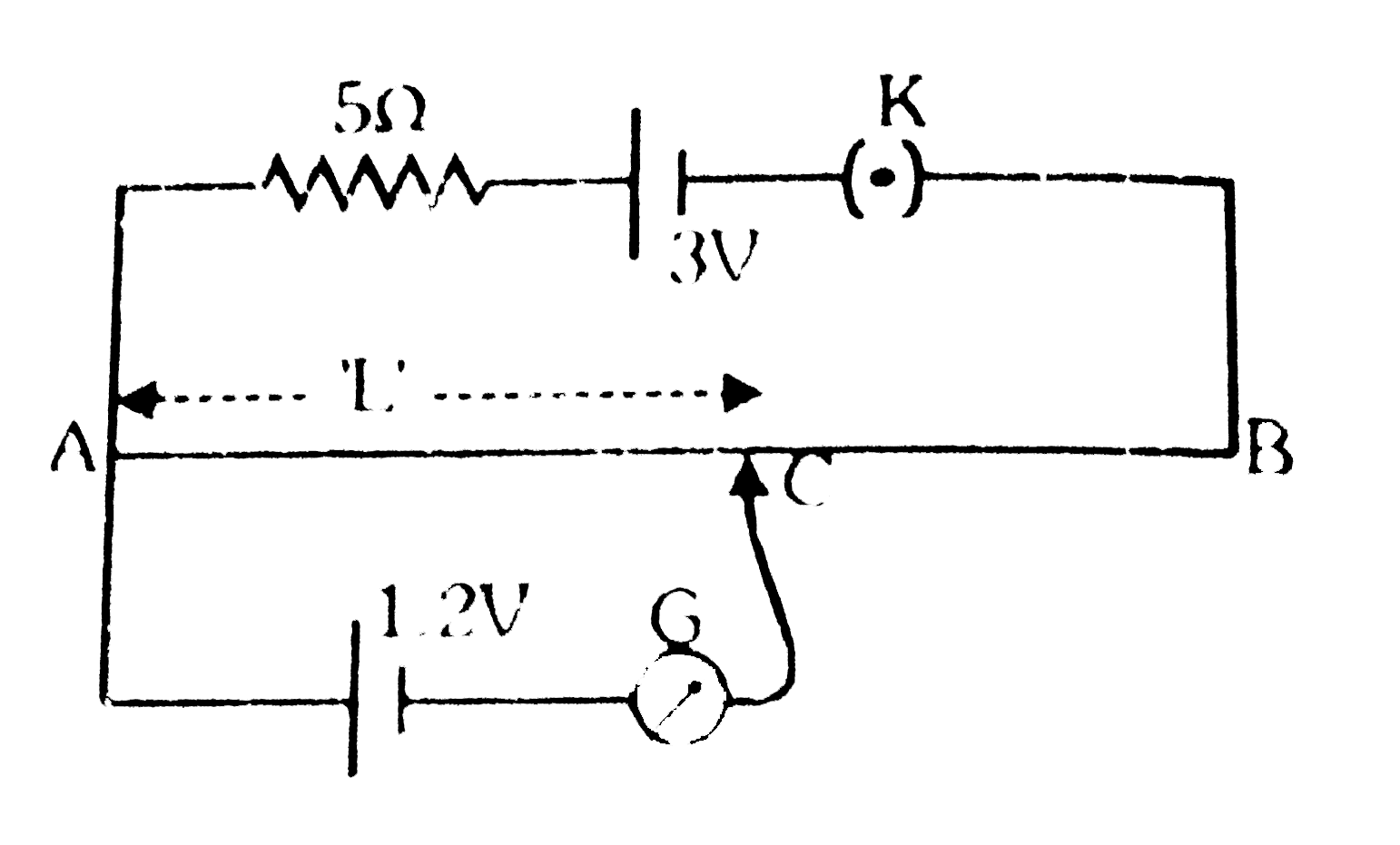
View SolutionThe potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance of 5Ω and an accumulaot or emf 3V having negligible resistance. A source 1.2V is balanced against a length 'L' of the potentionmeter wire. find the value of L.
View Solution
