A wire carrying a current i is first bent in the form of a square of side a and placed at right angle to a uniform magnetic field of induction B. The work done in changing its shape into a circle is
A) ia2B(π+2)
B) ia2B(π−2)
C) ia2B(4π−1)
D) ia2B(1−4π)
The correct Answer is:C
To solve the problem of calculating the work done in changing the shape of a wire from a square to a circle while carrying a current i in a magnetic field B, we can follow these steps:
Step 1: Determine the Area of the Square
The wire is initially bent into a square shape with each side of length a. The area As of the square is given by:
As=a2
Step 2: Calculate the Magnetic Moment of the Square
The magnetic moment μs of the square loop can be calculated using the formula:
μs=i×As=i×a2
Step 3: Determine the Circumference of the Square
The total length of the wire, which is also the perimeter of the square, is:
Ps=4a
Step 4: Find the Radius of the Circle
When the wire is reshaped into a circle, the circumference of the circle must equal the length of the wire:
C=2πr=4a
From this, we can solve for the radius r:
r=4a2π=2aπ
Step 5: Calculate the Area of the Circle
The area Ac of the circular loop is given by:
Ac=πr2=π(2aπ)2=π×4a2π2=4a2π
Step 6: Calculate the Magnetic Moment of the Circle
The magnetic moment μc of the circular loop is:
μc=i×Ac=i×4a2π
Step 7: Calculate the Change in Magnetic Moment
The change in magnetic moment Δμ when changing from the square to the circle is:
Δμ=μc−μs=(i×4a2π)−(i×a2)
Factoring out i:
Δμ=i(4a2π−a2)=ia2(4π−1)
Step 8: Calculate the Work Done
The work done W in changing the shape of the wire is given by the change in energy associated with the change in magnetic moment:
W=Δμ×B=ia2(4π−1)B
Final Result
Thus, the work done in changing the shape of the wire from a square to a circle is:
W=ia2B(4π−1)
The wire is initially bent into a square shape with each side of length a. The area As of the square is given by:
As=a2
The magnetic moment μs of the square loop can be calculated using the formula:
μs=i×As=i×a2
The total length of the wire, which is also the perimeter of the square, is:
Ps=4a
When the wire is reshaped into a circle, the circumference of the circle must equal the length of the wire:
C=2πr=4a
From this, we can solve for the radius r:
r=4a2π=2aπ
The area Ac of the circular loop is given by:
Ac=πr2=π(2aπ)2=π×4a2π2=4a2π
The magnetic moment μc of the circular loop is:
μc=i×Ac=i×4a2π
The change in magnetic moment Δμ when changing from the square to the circle is:
Δμ=μc−μs=(i×4a2π)−(i×a2)
Factoring out i:
Δμ=i(4a2π−a2)=ia2(4π−1)
The work done W in changing the shape of the wire is given by the change in energy associated with the change in magnetic moment:
W=Δμ×B=ia2(4π−1)B
Thus, the work done in changing the shape of the wire from a square to a circle is:
W=ia2B(4π−1)
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (MAGNETISM AND MATTER )
Explore 52 Videos
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (CUTTENT ELECTRICITY )
Explore 108 Videos
- ALTERNATING CURRENTBook:AAKASH SERIESChapter:ALTERNATING CURRENTExercise:EXERCISE - III
Explore 24 Videos
- APPENDICES (REVISION EXERCISE)Book:AAKASH SERIESChapter:APPENDICES (REVISION EXERCISE)Exercise:LAW OF MOTION
Explore 128 Videos
Similar Questions
A wire carrying current i is bent as shown in figure and placed in the plane of uniform magnetic field Bvec. The magnitude of magnetic force experienced by
View SolutionA wire carrying current l, bent in the form of a quarter circle is held at rest on a smooth table with two threads as shown. A uniform magnetic field exists in the region direction into the plane select the correct alternatives

View SolutionA wire PQR carrying a current l is bent as shown in the figure. It is placed in a uniform magnetic field B. What is the ratio of magnitude of the force on PQ to that on QR ?
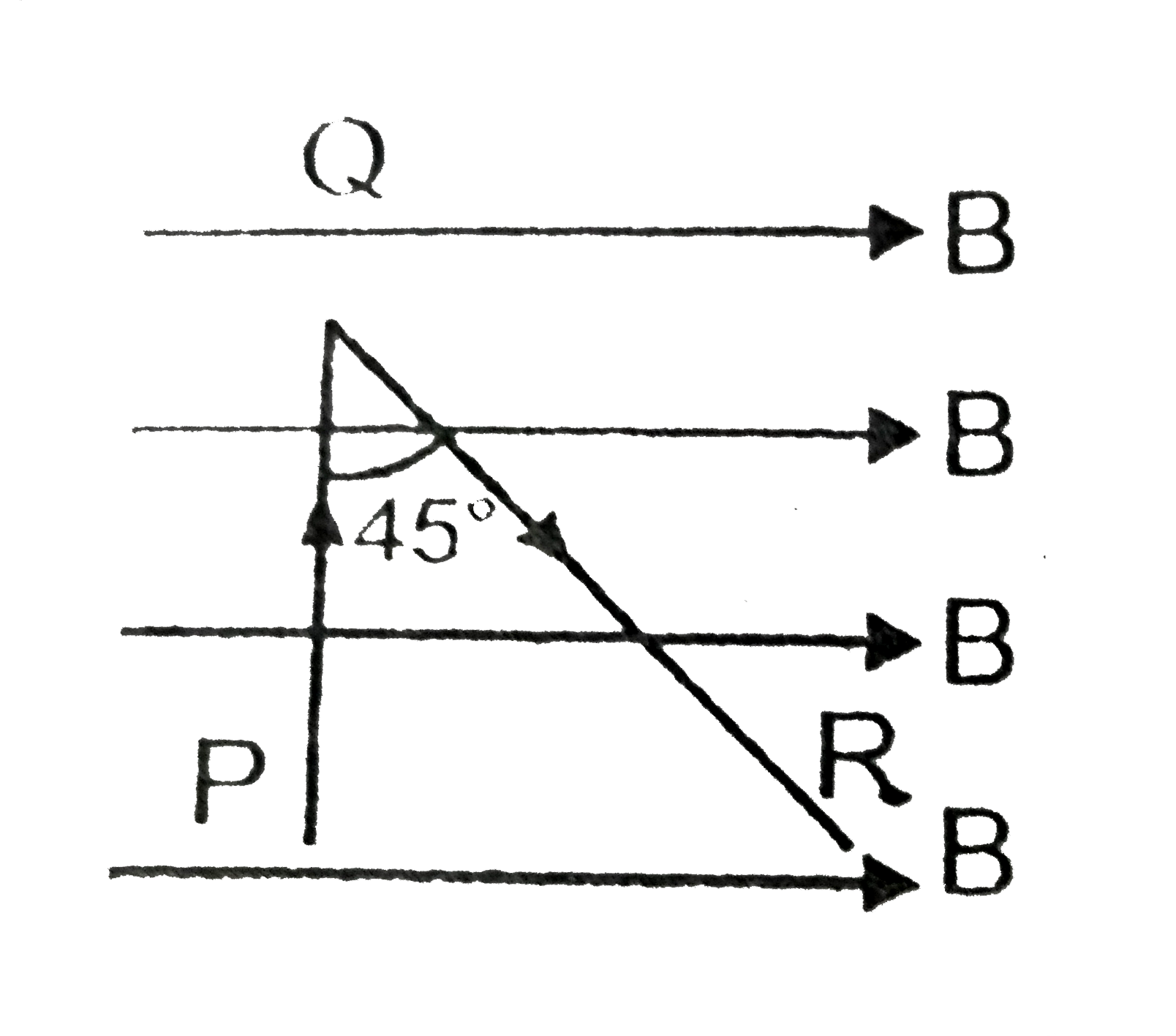
View Solution
A conducting wire MN carrying a current I is bent into the shape as shown and placed in xy plane. A uniform magnetic field →B=−Bˆk is existing in the region. The net magnetic force experenced by the conducting wire MN is
View Solutionthe force on current carrying wire placed in uniform magnetic field B as shown in figure is
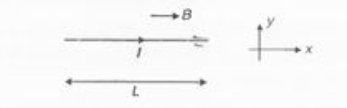
View SolutionA wire is bent in the form of an equilateral triangle of side 1m and carries a current of 2A.. It is placed in a magnetic field of induction 2.0 T directed into the plane of paper. The direction and magnitude of magnetic force acting on each side of the triangle will be
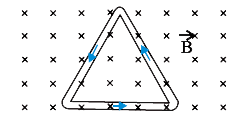
View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionA metallic wire is folded to form a square loop a side 'a'. It carries a current 'I' and is kept perpendicular to a uniform magnetic field. If the shape of the loop is changed from square to a circle without changing the length of thw wire and current, the amount of work done in doing so is
View SolutionA wire is bent in the form of a V shape and placed in a horizontal plane.There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
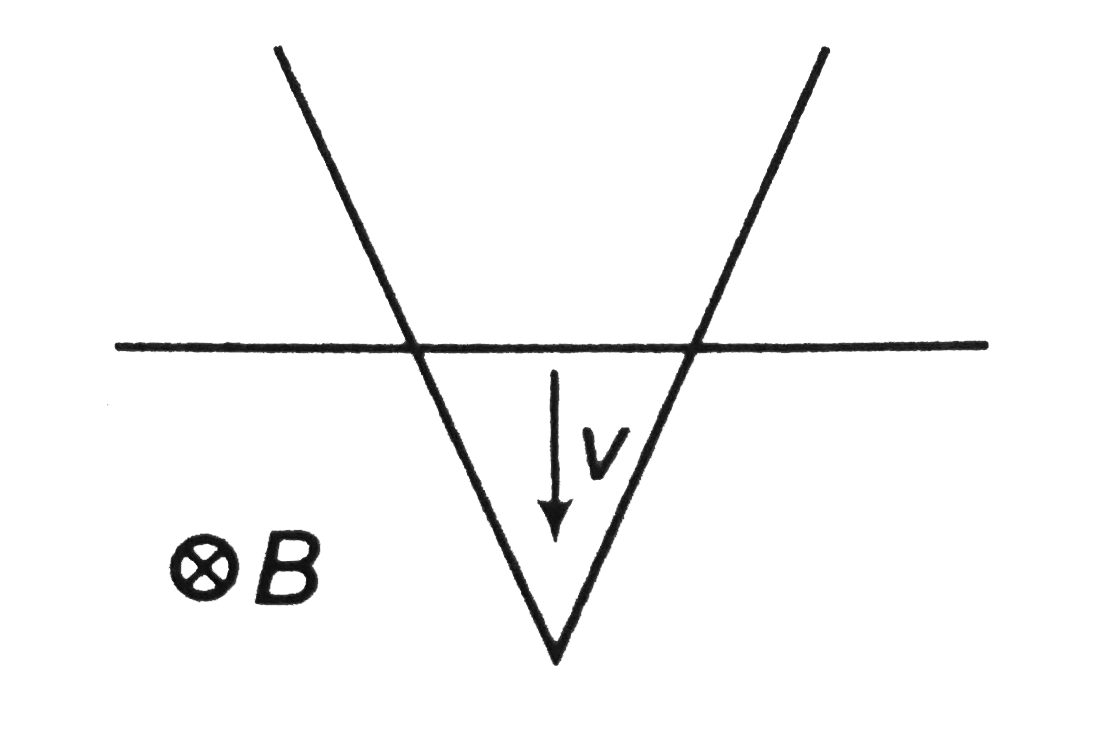
View SolutionA wires PQRS carrying a current I runs along three edges of a cube of side l as shown in figure. There exists a uniform magnetic field of magnitude B along one of the sides of cube. The magnitude of the force acting on the wire is
View Solution

