A current carrying circular coil of radius 11 cm is placed with its plane in magnetic meridian. The resultant magnetic induction at the centre of the coil is (Given current in the coil is 7A and BH=0.4Gauss ]
3×10−5T
4×10−5T
4√2×10−5T
0
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- Radius of the coil, R=11cm=11×10−2m
- Current in the coil, I=7A
- Horizontal magnetic induction, BH=0.4Gauss=0.4×10−4Tesla=4×10−5Tesla
Step 2: Calculate the magnetic field due to the coil at its center
The formula for the magnetic field B at the center of a circular coil is given by:
B2=μ04π⋅IR
Where:
- μ0=4π×10−7T m/A (permeability of free space)
Substituting the values:
B2=4π×10−74π⋅711×10−2
The 4π cancels out:
B2=10−7⋅711×10−2=7×10−511
Calculating B2:
B2≈6.36×10−5Tesla
Step 3: Calculate the resultant magnetic induction at the center of the coil
The resultant magnetic induction Bnet is given by:
Bnet=√B21+B22
Where:
- B1=BH=4×10−5Tesla
- B2≈6.36×10−5Tesla
Substituting the values:
Bnet=√(4×10−5)2+(6.36×10−5)2
Calculating Bnet:
Bnet=√(16×10−10)+(40.45×10−10)
Bnet=√56.45×10−10≈7.51×10−5Tesla
Step 4: Final Result
The resultant magnetic induction at the center of the coil is approximately 7.51×10−5Tesla.
---
- Radius of the coil, R=11cm=11×10−2m
- Current in the coil, I=7A
- Horizontal magnetic induction, BH=0.4Gauss=0.4×10−4Tesla=4×10−5Tesla
The formula for the magnetic field B at the center of a circular coil is given by:
B2=μ04π⋅IR
Where:
- μ0=4π×10−7T m/A (permeability of free space)
B2=4π×10−74π⋅711×10−2
The 4π cancels out:
B2=10−7⋅711×10−2=7×10−511
Calculating B2:
B2≈6.36×10−5Tesla
The resultant magnetic induction Bnet is given by:
Bnet=√B21+B22
Where:
- B1=BH=4×10−5Tesla
- B2≈6.36×10−5Tesla
Bnet=√(4×10−5)2+(6.36×10−5)2
Calculating Bnet:
Bnet=√(16×10−10)+(40.45×10−10)
Bnet=√56.45×10−10≈7.51×10−5Tesla
The resultant magnetic induction at the center of the coil is approximately 7.51×10−5Tesla.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
Current 'i' is flowing in heaxagonal coil of side a. The magnetic induction at the centre of the coil will be
View SolutionA vertical circular coil of one turn and radius 9.42 cm is placed with its plane in the magnetic meridian and short magnetic needle is pivoted at the centre of the coil so that it can freely rotate in the horizontal plane. If a current of 6A is passed through the coil, then the needle deflects by (BH=4×10−5T)
View SolutionThe magnetic field at the centre of the current carrying coil is
View SolutionThe current through a circular coil appears to be flowing in clock-wise direction for an observer. The magnetic induction at the centre of the coil is:
View SolutionA current I enters a uniform circular coil of radius R, branches into two parts and then recombines as shown in the circuit diagram. The resultant magnetic field at the centre of the coil is :
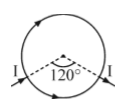
View SolutionA circular coil of average radius 6 cm has 20 turns. A current 1.0 A is set up through it. Find the magnetic induction at
(i) The centre of the coil
View SolutionA circular coil of radius 1⋅5cmcarriesacurrentof1⋅5A. If the coil has 25 turns , find the magnetic field at the centre.
View SolutionA current I flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field, magnitude of the torque that acts on the coil is
View SolutionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is

View SolutionA circular coil of radius r having number of turns n and carrying a current A produces magnetic induction at its centre of magnitude B. B can be doubled by
View Solution
