The specific resistance of the material of a wire is 'ρ' and its volume is 3m3 and its resistance is 3Ω. The length of the wire will be
1(√ρ)
3√(ρ)
√3ρ
ρ√3
The correct Answer is:B
To find the length of the wire given its specific resistance (ρ), volume (V), and resistance (R), we can follow these steps:
Step 1: Understand the relationship between volume, area, and length
The volume (V) of the wire can be expressed in terms of its cross-sectional area (A) and length (L):
V=A×L
Given that the volume V=3m3, we can express the area in terms of length:
A=VL=3L
Step 2: Use the formula for resistance
The resistance (R) of the wire is given by the formula:
R=ρLA
Substituting the expression for area from Step 1 into this formula gives:
R=ρL3L
This simplifies to:
R=ρL23
Step 3: Substitute the known resistance value
We know that the resistance R=3Ω. Therefore, we can set up the equation:
3=ρL23
Step 4: Solve for L2
To isolate L2, multiply both sides by 3:
9=ρL2
Now, rearranging gives:
L2=9ρ
Step 5: Take the square root to find L
Taking the square root of both sides to find the length L:
L=√9ρ
This simplifies to:
L=3√ρ
Final Result
Thus, the length of the wire is:
L=3√ρ
---
The volume (V) of the wire can be expressed in terms of its cross-sectional area (A) and length (L):
V=A×L
Given that the volume V=3m3, we can express the area in terms of length:
A=VL=3L
The resistance (R) of the wire is given by the formula:
R=ρLA
Substituting the expression for area from Step 1 into this formula gives:
R=ρL3L
This simplifies to:
R=ρL23
We know that the resistance R=3Ω. Therefore, we can set up the equation:
3=ρL23
To isolate L2, multiply both sides by 3:
9=ρL2
Now, rearranging gives:
L2=9ρ
Taking the square root of both sides to find the length L:
L=√9ρ
This simplifies to:
L=3√ρ
Thus, the length of the wire is:
L=3√ρ
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
Specific resistance of a wire depends on its
View SolutionSpecific resistance of a wire depends on its
View SolutionThe temperature coefficient of resistance of a wire is 0.00125 per ∘C. At 300 K, its resistance is 1Ω. The resistance of the wire will be 2Ω at
View SolutionTemperature coefficient of resistance of a wire at 0∘C is 0.00125∘C−1 . At 25∘C its resistance is 1Ω . The resitance of the wire will be 1.2Ω at
View SolutionThe temperature coefficient of resistance of the material of a wire is 0.00125∘C−1. Its resistance at 27∘C is 1Ω. At what temperature will its resistance be 2Ω ?
View SolutionThe resistance of a wire R Ω . The wire is stretched to double its length keeping volume constant. Now, the resistance of the wire will become
View SolutionIf a wire is stretched to double its length, find the new resistance if the original resistance of the wire was R.
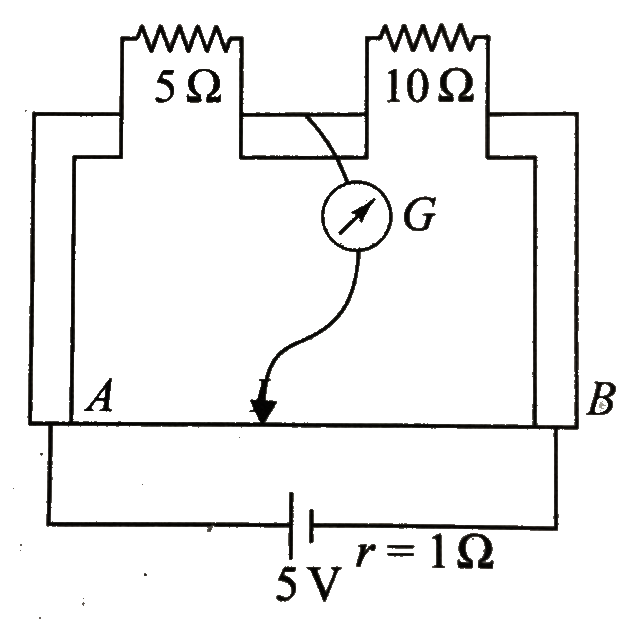
View SolutionIn a meter bridge circuit, the two resistances in the gap are 5Ω and 10Ω. The wire resistance is 4Ω. The emf of the cell connected at the ends of the wire is 5V and its internal resistance is 1Ω. What current will flow through the galvenometer of resistance 30Ω if the contact is made at the midpoint of wire ?
View SolutionThe resistance of a thin silver wire is 1.0Ω at 20∘C. The wire is placed in a liquid bath and its resistance rises to 1.2Ω. What is the temperature of the bath? α for silver is 3.8×10−3/(.∘C)
View SolutionThe resistance of a wire is R ohm. If it is melted and stretched to n times its original length, its new resistance will be
View Solution
