A parallel plate capacitor of capacity 100μF is charged by a battery of 50 volts. The battery remains connected and if the plates of the capacitor are separated so that the distance between them becomes double the original distance, the additional energy given by the battery to the capacitor in joules is
A) 62.5×10−3
B) 12.5×10−3
C) 1.25×10−3
D) 0.125×10−3
The correct Answer is:A
To solve the problem step by step, we will calculate the initial and final energy of the capacitor and then find the additional energy given by the battery when the distance between the plates is doubled.
Step 1: Calculate the Initial Energy of the Capacitor
The initial energy U1 stored in a capacitor is given by the formula:
U1=12CV2
Where:
- C=100μF=100×10−6F
- V=50V
Substituting the values:
U1=12×(100×10−6)×(50)2
Calculating (50)2:
(50)2=2500
Now substituting this back:
U1=12×(100×10−6)×2500
U1=12×250×10−3=125×10−3J=0.125J
Step 2: Determine the New Capacitance After Doubling the Distance
The capacitance C of a parallel plate capacitor is given by:
C=ε0Ad
When the distance d is doubled, the new capacitance C′ becomes:
C′=ε0A2d=12C
Thus:
C′=12×100μF=50μF=50×10−6F
Step 3: Calculate the Final Energy of the Capacitor
The final energy U2 stored in the capacitor when the battery is still connected is:
U2=12C′V2
Substituting the values:
U2=12×(50×10−6)×(50)2
Calculating:
U2=12×(50×10−6)×2500
U2=12×125×10−3=62.5×10−3J=0.0625J
Step 4: Calculate the Additional Energy Given by the Battery
The additional energy given by the battery is the difference between the initial and final energy:
Additional Energy=U1−U2
Substituting the values:
Additional Energy=(0.125J)−(0.0625J)=0.0625J
Final Answer
The additional energy given by the battery to the capacitor is:
Additional Energy=0.0625J
The initial energy U1 stored in a capacitor is given by the formula:
U1=12CV2
Where:
- C=100μF=100×10−6F
- V=50V
U1=12×(100×10−6)×(50)2
Calculating (50)2:
(50)2=2500
Now substituting this back:
U1=12×(100×10−6)×2500
U1=12×250×10−3=125×10−3J=0.125J
The capacitance C of a parallel plate capacitor is given by:
C=ε0Ad
When the distance d is doubled, the new capacitance C′ becomes:
C′=ε0A2d=12C
Thus:
C′=12×100μF=50μF=50×10−6F
The final energy U2 stored in the capacitor when the battery is still connected is:
U2=12C′V2
Substituting the values:
U2=12×(50×10−6)×(50)2
Calculating:
U2=12×(50×10−6)×2500
U2=12×125×10−3=62.5×10−3J=0.0625J
The additional energy given by the battery is the difference between the initial and final energy:
Additional Energy=U1−U2
Substituting the values:
Additional Energy=(0.125J)−(0.0625J)=0.0625J
The additional energy given by the battery to the capacitor is:
Additional Energy=0.0625J
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
A parallel plate capacitor is charged and then the battery is disconnected. When the plates of the capacitor are brought closer, then
View SolutionA parallel plate capacitor is charged and the charging battery is then disconnected. If the plates of the capacitor are moved farther apart by means of insulating handles:
View Solution
Knowledge Check
A parallel plate capacitor without any dielectric within its plates, has a capacitance C, and is connected to a battery of emf V. The battery is disconnected and the plates of the capacitor are pulled apart until the separation between the plates is doubled. What is the work done by the agent pulling the plates apart, in this process ?
A12CV2B32CV2C−32CV2DCV2A parallel plate condenser is charged by connected it to a battery. The battery is disconnected and a glass slab is introduced between the plates. Then
Apotential increasesBelectric intensity increasesCenergy decreases.Dcapacity decreases
A parallel plate air capacitor is connected to a battery. After charging fully, the battery is disconnected and the plates are pulled apart to increase their separation. Which of the following statements is correct ?
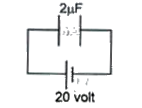
View SolutionIn the figure a capacitor of capacitance 2μF is connected to a cell of emf 20 volt. The plates of the capacitor are drawn apart slowly to double the distance between them. The work done by the external agent on the plates is:
View SolutionA parallel plate capacitor is connected across a battery. Now, keeping the battery connected, a dielectric slab is inserted between the plates. In the process,
View SolutionA parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would (i) the capacitance, (ii) the electric field between the plates and (iii) the energy stored in the capacitor, be affected ? Justify your answer.
View SolutionA parallel plate capacitor is charged by a battery. After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates. How will (i) the capacitance of the capacitor, (ii) potential difference between the plates and (iii) the energy stored in the capacitor be affected ?
Justify your answer in each case.
View SolutionA capacitor having capacity of 2μF is charged to 200V and then the plates of the capacitor are connected to a resistance wire. The heat produced in joule will be
View Solution
