The refractive index of denser medium with respect to rarer medium is 1.125. The difference between the velocities of light in the two media is 0.25×108m/s. Find the velocities of light in the two media. (c=3×108m/s).
To find the velocities of light in the two media, we can follow these steps:
Step 1: Understand the given information
We know:
- The refractive index of the denser medium with respect to the rarer medium is n=1.125.
- The difference in velocities of light in the two media is Δv=0.25×108m/s.
- The speed of light in vacuum is c=3×108m/s.
Step 2: Define the velocities in the two media
Let:
- v1 = velocity of light in the denser medium
- v2 = velocity of light in the rarer medium
From the definition of refractive index:
n=cv
Thus, we can express the velocities as:
v1=cn1andv2=cn2
Step 3: Relate the velocities using the refractive index
Since the refractive index of the denser medium with respect to the rarer medium is given by:
n1n2=1.125
This implies:
n1=1.125⋅n2
Using the relationship of velocities:
v1v2=n2n1
Substituting n1:
v1v2=n21.125⋅n2=11.125
Thus, we can express v1 in terms of v2:
v1=v21.125
Step 4: Set up the equation based on the difference in velocities
We know that:
v2−v1=0.25×108
Substituting v1:
v2−v21.125=0.25×108
Step 5: Solve for v2
Factor out v2:
v2(1−11.125)=0.25×108
Calculating 1−11.125:
1−11.125=1−0.8889=0.1111
Thus, we have:
v2⋅0.1111=0.25×108
Now, solving for v2:
v2=0.25×1080.1111≈2.25×108m/s
Step 6: Calculate v1
Now that we have v2, we can find v1:
v1=v21.125=2.25×1081.125≈2.00×108m/s
Final Result
The velocities of light in the two media are:
- v1≈2.00×108m/s (in the denser medium)
- v2≈2.25×108m/s (in the rarer medium)
We know:
- The refractive index of the denser medium with respect to the rarer medium is n=1.125.
- The difference in velocities of light in the two media is Δv=0.25×108m/s.
- The speed of light in vacuum is c=3×108m/s.
Let:
- v1 = velocity of light in the denser medium
- v2 = velocity of light in the rarer medium
n=cv
Thus, we can express the velocities as:
v1=cn1andv2=cn2
Since the refractive index of the denser medium with respect to the rarer medium is given by:
n1n2=1.125
This implies:
n1=1.125⋅n2
v1v2=n2n1
Substituting n1:
v1v2=n21.125⋅n2=11.125
Thus, we can express v1 in terms of v2:
v1=v21.125
We know that:
v2−v1=0.25×108
Substituting v1:
v2−v21.125=0.25×108
Factor out v2:
v2(1−11.125)=0.25×108
Calculating 1−11.125:
1−11.125=1−0.8889=0.1111
Thus, we have:
v2⋅0.1111=0.25×108
Now, solving for v2:
v2=0.25×1080.1111≈2.25×108m/s
Now that we have v2, we can find v1:
v1=v21.125=2.25×1081.125≈2.00×108m/s
The velocities of light in the two media are:
- v1≈2.00×108m/s (in the denser medium)
- v2≈2.25×108m/s (in the rarer medium)
Topper's Solved these Questions
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:PROBLEMS ( LEVEL-II)
Explore 60 Videos
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:EXERCISE (VERY SHORT ANSWER QUESTIONS )
Explore 53 Videos
- PRACTICAL PHYSICSBook:AAKASH SERIESChapter:PRACTICAL PHYSICSExercise:LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
Explore 4 Videos
- SEMICONDUCTOR DEVICESBook:AAKASH SERIESChapter:SEMICONDUCTOR DEVICESExercise:EXERCISE - III
Explore 3 Videos
Similar Questions
If the speed of light in diamond is 1.24×108 m/s, find its refractive index.
View SolutionRefractive index of glass with respect to medium is 43. If vm−vg=6.25×107 m/s., then velocity of light in medium is
View SolutionThe refractive index of glass with respect to water is 98. If the velocity of wavelength of light in glass are 2×108m/s and 4000 Å respectively, find the velocity and wavelength of light in water.
View SolutionIf the refractive index of glass is 1.5. Find the velocity of light in glass. (Velocity of light in vacuum =3×108m/s)
View SolutionWhat is the refractive index in a medium where the speed of light is 1.5×108 m/s ?
View SolutionThe refractive index of a medium 'x' with respect to a medium 'y' is 23 and the refractive index of medium 'y' with respect to medium 'z' is 43. Find the refractive index of medium 'z' with respect to medium 'x' . If the speed of light in medium 'x' is 3×108ms−1, Calculate the speed of light in medium 'y'.
View SolutionWhat is the velocity of the light in the medium if Sin θi=0.707 , Sin θr=0.500 , and the velocity of light in a vacuum is 3.0×108 m/sec ?
View SolutionA ray of light is incident on a medium with angle of incidence I and refracted into a second medium with angle of refraction r. The graph of sin(i)vssin(R) is as shown in figure. Then the velocity of light in the first medium in n times the velocity of light in the second medium. What shoul be th evalue of n?
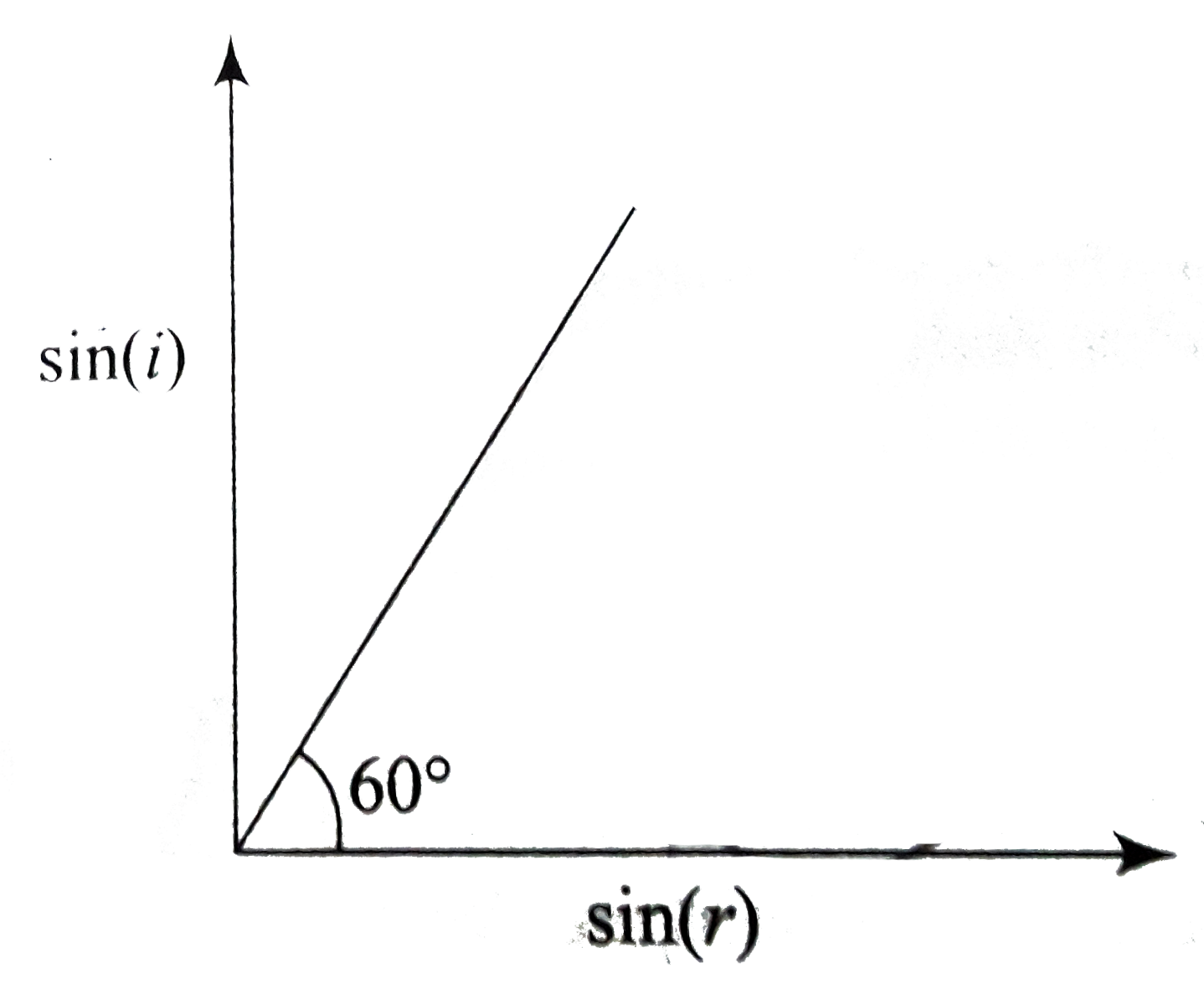
View SolutionThe velocities of light in two different media are 2*108m/s and 2.5 * 108m/s respectively.The critical angle for these media is
View SolutionThe speed of light in air is 3×108 m/s and the speed of light in glass is 2×108 m/s. What is the refractive index of glass?
View Solution

