The equation of refraction at a spherical surface is
Taking R= infinity , show that this equation leads to the equation for refraction at a plane surface .
To show that the equation of refraction at a spherical surface leads to the equation for refraction at a plane surface, we start with the given equation:
μ2v−μ1u=μ2−μ1R
Step 1: Set R=∞
When we consider a plane surface, the radius of curvature R approaches infinity. Therefore, we substitute R with infinity in the equation:
μ2v−μ1u=μ2−μ1∞
Step 2: Simplify the Right Side
Since μ2−μ1∞=0, the equation simplifies to:
μ2v−μ1u=0
Step 3: Rearrange the Equation
Rearranging the equation gives us:
μ2v=μ1u
Step 4: Cross-Multiply
Cross-multiplying the terms results in:
μ2⋅u=μ1⋅v
Step 5: Relate Real Depth and Apparent Depth
In the context of refraction, we define:
- u as the real depth (the actual distance from the object to the surface),
- v as the apparent depth (the distance from the observer to the image).
Thus, we can express u and v in terms of the real and apparent depths:
μ2⋅(real depth)=μ1⋅(apparent depth)
Step 6: Write the Final Relation
Rearranging gives us the relation:
real depthapparent depth=μ1μ2
This is the required equation for refraction at a plane surface.
Conclusion
Thus, we have shown that when R=∞, the equation of refraction at a spherical surface leads to the equation:
real depthapparent depth=μ1μ2
- u as the real depth (the actual distance from the object to the surface),
- v as the apparent depth (the distance from the observer to the image).
Topper's Solved these Questions
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:EXERCISE (VERY SHORT ANSWER QUESTIONS )
Explore 53 Videos
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:PROBLEMS ( LEVEL-I)
Explore 57 Videos
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:EXERCISE (LONG ANSWER QUESTIONS )
Explore 9 Videos
- PRACTICAL PHYSICSBook:AAKASH SERIESChapter:PRACTICAL PHYSICSExercise:LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
Explore 4 Videos
- SEMICONDUCTOR DEVICESBook:AAKASH SERIESChapter:SEMICONDUCTOR DEVICESExercise:EXERCISE - III
Explore 3 Videos
Similar Questions
Is the formula "Real depth/Apparent depth =μ. valid if viewed from a position quite away from the normal ?
View SolutionIdentify the statements are True of False.
a. The equation μ2v−μ1u=μ12−μ1R is applicabel to a plane surface for R=∞ .
h. In the above equation, μ1 is medium in which the object is placed and μ2 is the medium in which the image is formed.
c. In the figure shown, the real image of object O is formed at a distance 5R in the medium.

d. In figure, the image of an object O place on the center face of the sphere is formed at infinity,.
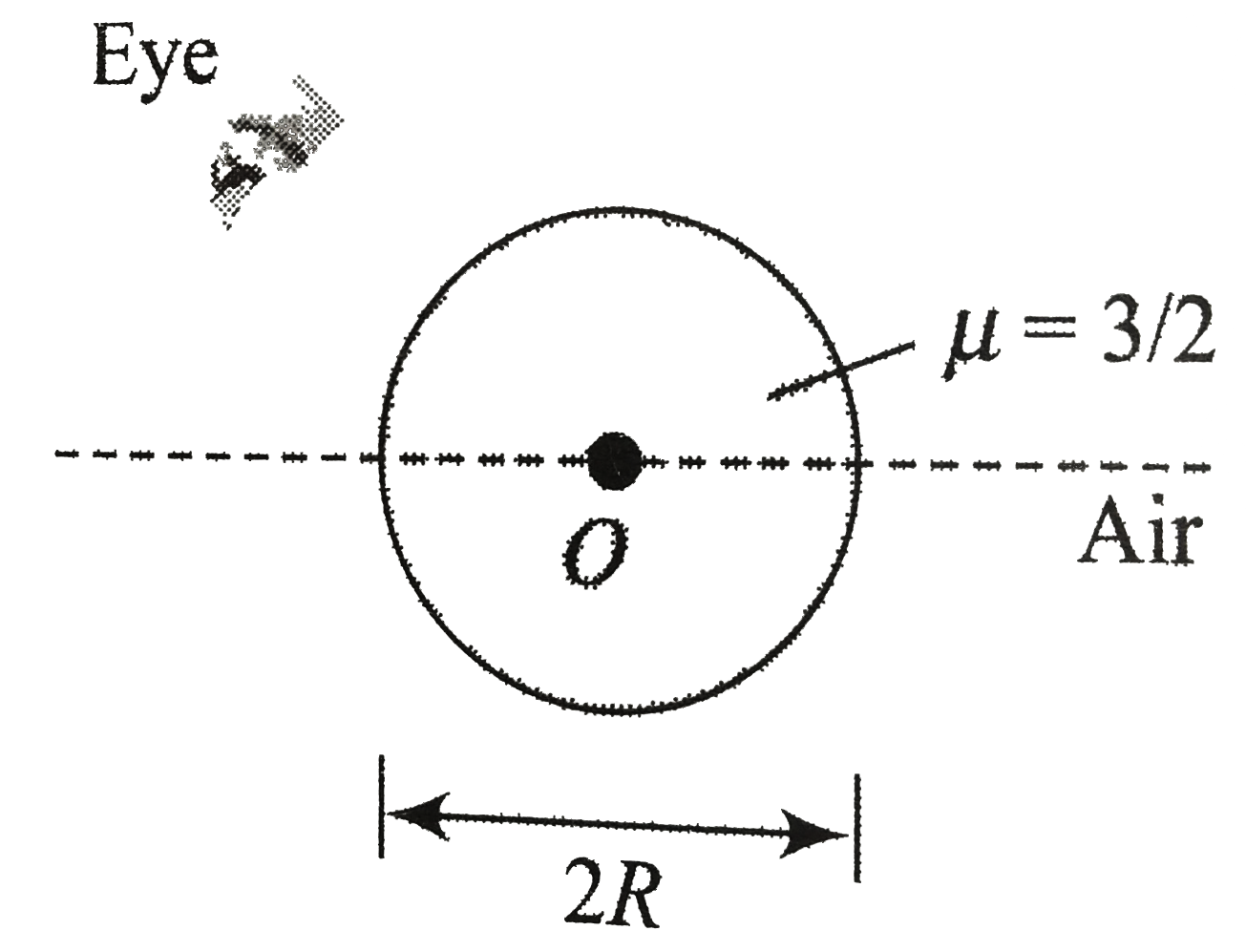
e. In fig , the image of an object O placed on the opposite face of the sphere is foremd at infinity.
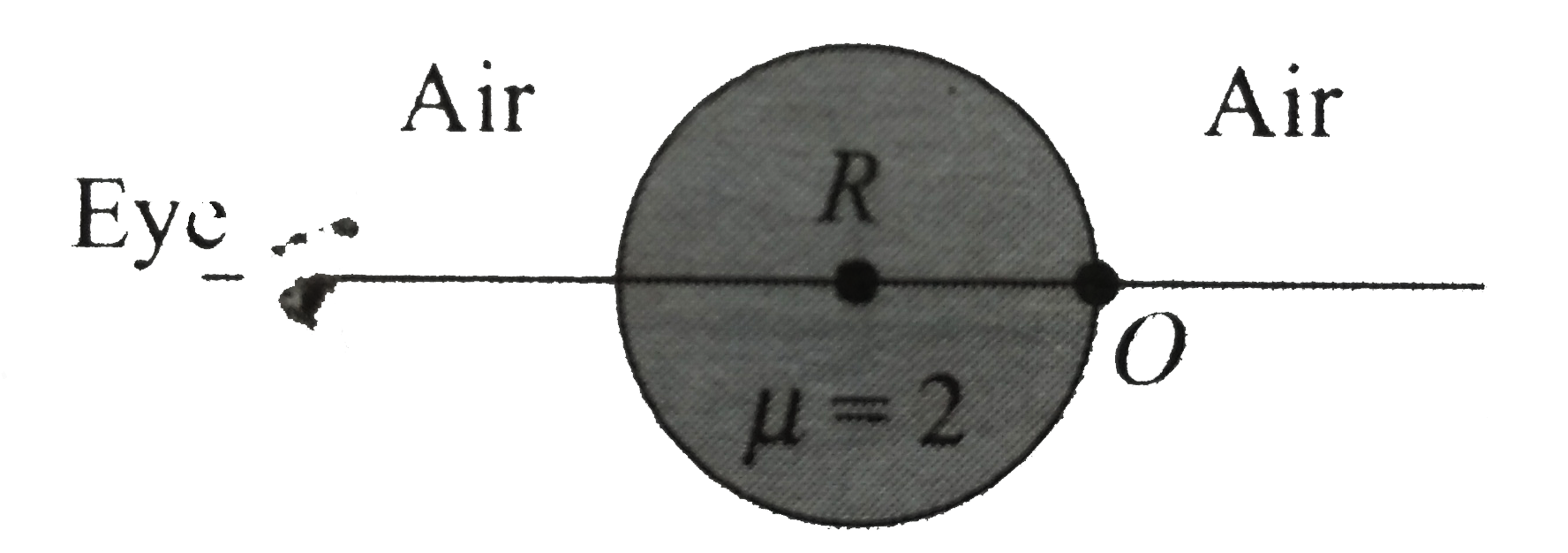
View SolutionThe figure shows a ray incident a angle i=π/3 of the plot drawn shown the variartion of |r−i|versusμ1μ2=k,(r=angle of refraction)

the value ofk1is
View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
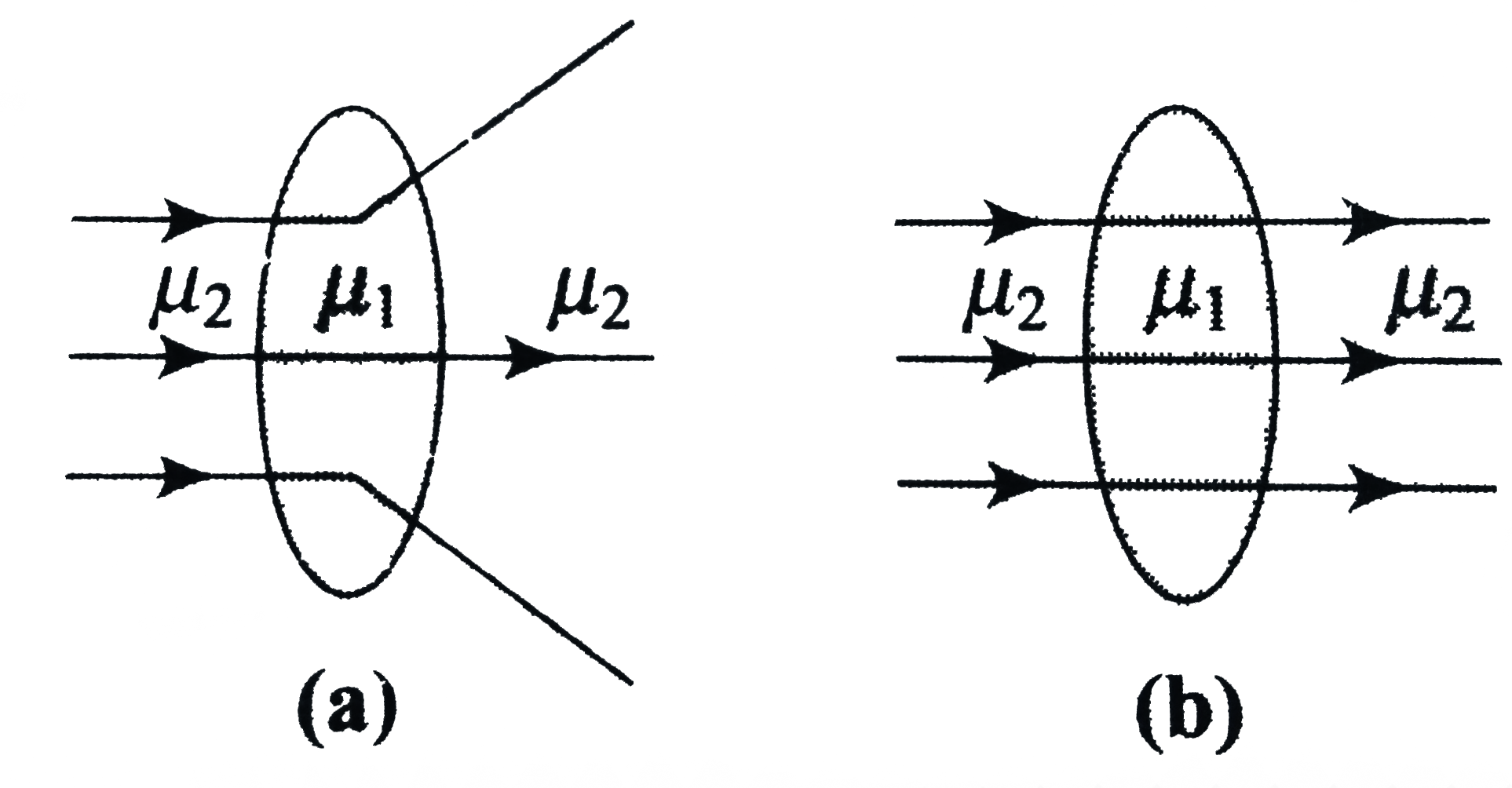
View SolutionIn above question if observer is in medium μ3 what is the apparenet depth of object seen below surface 1CD.
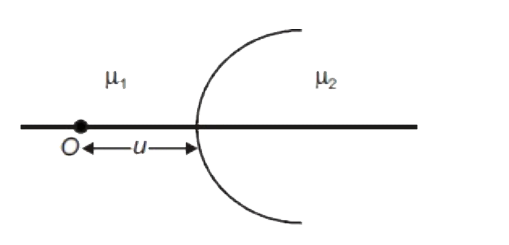
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
View SolutionMonochramatic light is incident on the pLane interface AB between two media of refractive indices μ1 and μ2(μ2>μ1) at an angle of incidence theta as shown in figure. The angle theta is infinitesimally greater thannte critical angle for the two media so thast total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive inde μ2 is introduced on theinterface (as shown in figure ) , show that for any value of μ2 all light will ultimately be reflected back into medium II.
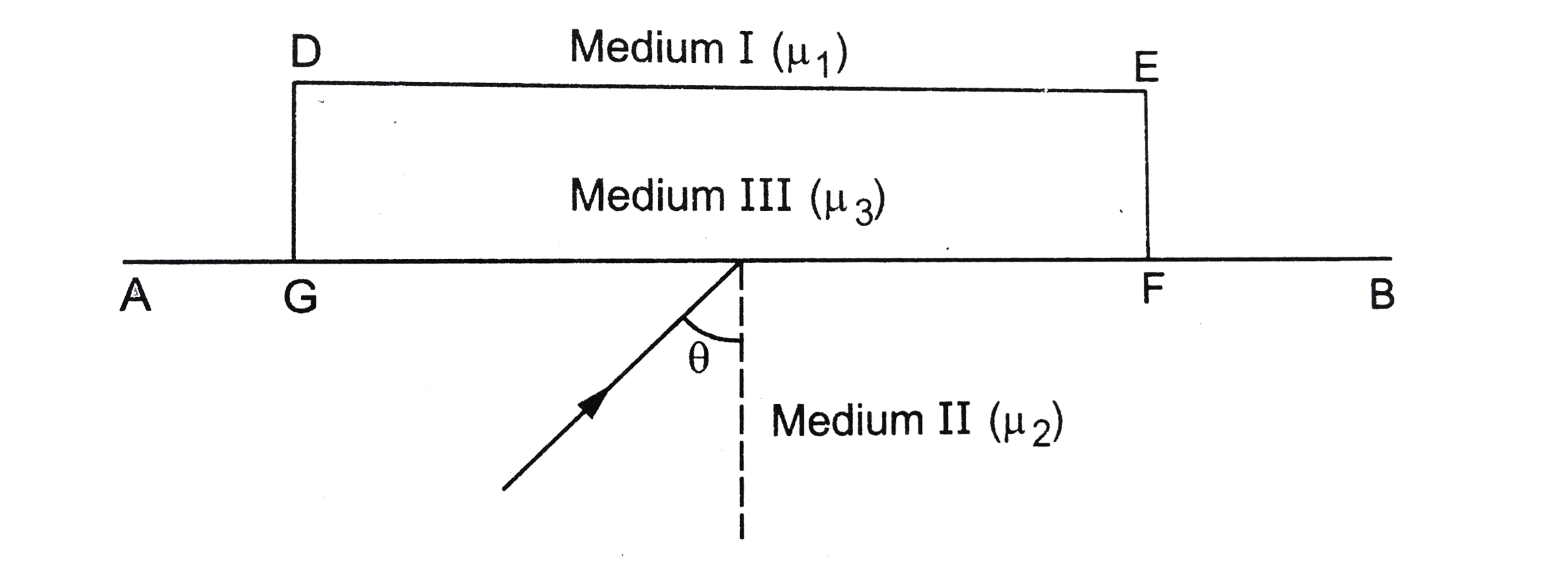
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
View SolutionThe radii of curvature of two spherical surfaces of a concave convex lens (μ=1.5) are 20 cm and 40 cm. (i) What is its focal length when it is in air? Also find its focal length when it is immersed in a liquid of refractive index (ii) μ=1.2 (iii) μ=2
View SolutionObtain an expression for refraction at a single convex spherical surface separating the two media having refractive indices μ1(rarer medium) and μ2(denser medium) i.e., a relation between u,v,μ1,μ2 and R.
View Solution

