A plane wave that falls on a barrier containing small circular opening of dimension d. What can be said about the behaviour of the wave if
To analyze the behavior of a plane wave that falls on a barrier with a small circular opening of dimension d, we will consider three different scenarios based on the relationship between the wavelength λ and the dimension d of the opening.
1. Case (i): λ≪d (Wavelength much smaller than the aperture dimension)
- When the wavelength is much smaller than the aperture dimension, the wave behaves almost like a ray. The wavefronts pass through the opening with minimal diffraction. The majority of the wave energy continues in the original direction, and the diffraction effects are negligible.
- Conclusion: The wave will pass through the opening with little to no diffraction.
2. Case (ii): λ=d (Wavelength equal to the aperture dimension)
- In this case, the wavelength is comparable to the dimension of the aperture. This is the ideal scenario for diffraction. The wave will spread out significantly after passing through the opening, leading to noticeable diffraction patterns. The wavefronts will begin to diverge as they exit the aperture.
- Conclusion: The wave will undergo significant diffraction, producing a distinct diffraction pattern.
3. Case (iii): λ≫d (Wavelength much greater than the aperture dimension)
- Here, the wavelength is much larger than the aperture dimension. The wave will experience strong diffraction. The wavefronts will spread out widely after passing through the opening, and the diffraction effects will dominate. The wave will behave more like a point source of waves emanating from the aperture.
- Conclusion: The wave will diffract extensively, resulting in a broad spread of the wavefronts.
Summary of Results:
- For λ≪d: Minimal diffraction; wave passes through the opening almost unaffected.
- For λ=d: Significant diffraction; formation of a diffraction pattern.
- For λ≫d: Extensive diffraction; wave behaves like a point source.
- When the wavelength is much smaller than the aperture dimension, the wave behaves almost like a ray. The wavefronts pass through the opening with minimal diffraction. The majority of the wave energy continues in the original direction, and the diffraction effects are negligible.
- Conclusion: The wave will pass through the opening with little to no diffraction.
- In this case, the wavelength is comparable to the dimension of the aperture. This is the ideal scenario for diffraction. The wave will spread out significantly after passing through the opening, leading to noticeable diffraction patterns. The wavefronts will begin to diverge as they exit the aperture.
- Conclusion: The wave will undergo significant diffraction, producing a distinct diffraction pattern.
- Here, the wavelength is much larger than the aperture dimension. The wave will experience strong diffraction. The wavefronts will spread out widely after passing through the opening, and the diffraction effects will dominate. The wave will behave more like a point source of waves emanating from the aperture.
- Conclusion: The wave will diffract extensively, resulting in a broad spread of the wavefronts.
- For λ≪d: Minimal diffraction; wave passes through the opening almost unaffected.
- For λ=d: Significant diffraction; formation of a diffraction pattern.
- For λ≫d: Extensive diffraction; wave behaves like a point source.
Topper's Solved these Questions
- WAVE OPTICSBook:AAKASH SERIESChapter:WAVE OPTICSExercise:EXERCISE (LONG ANSWER QUESTIONS (INTERFERENCE))
Explore 4 Videos
- WAVE OPTICSBook:AAKASH SERIESChapter:WAVE OPTICSExercise:EXERCISE (LONG ANSWER QUESTIONS (DIFFRACTION))
Explore 1 Video
- WAVE OPTICSBook:AAKASH SERIESChapter:WAVE OPTICSExercise:ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED ) Straight Objective Type Questions)
Explore 12 Videos
- WAVE MOTION AND SOUNDBook:AAKASH SERIESChapter:WAVE MOTION AND SOUNDExercise:PROBLEMS (LEVEL - II)
Explore 97 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-III (Doppler effect :)
Explore 15 Videos
Similar Questions
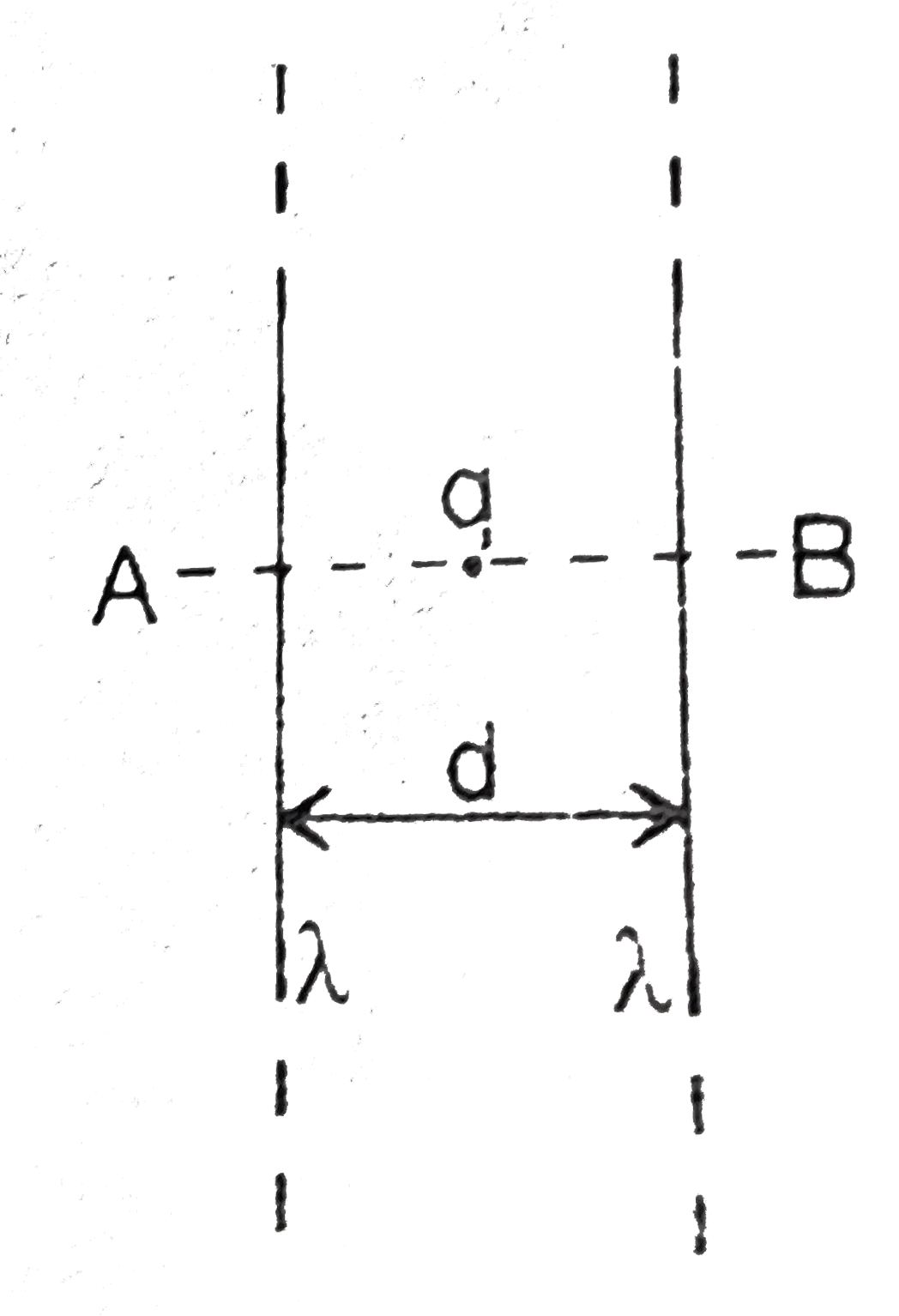
Two infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q and the outer shell has charge +4q.
(i) What is the total charge on the (a) inner surface of the small shell, (b) outer surface of the small shell (c) inner surface of the large shell, (d) outer surface of the large shell ?
(ii) Calculate the electric field in terms of q and the the distance r from the common centre of two shells for (a) r<a, (b) a<r<b, (c) b<r<c, (d) c<r<d, (e) r>d

View SolutionConsider a coaxial system of two thin convex lenses of focal length f each separated by a distance d. Draw ray diagrams for image formation corresponding to an object at infinity placed on the principal axis in the following cases: (a) d<f,(b)d=f, (c ) f<d<2f, (d) d=2f, and (e) d>2f. Indicate the nature of the combination (concave, convex or plane) in each case.
View SolutionArrange the following in order of increasing masses.
i. 1 molecules of oxygen ii. 1 atom of nitrogen
iii. 1 mol of water iv. 1×10−10 of iron
a. ii lt I lt iii lt iv b. ilt iilt ivlt iii
c. ii lt ilt ivlt iii d. iltiiltiiiltiv
View SolutionLet l=sinθ,m=cosθandn=tanθ.
Q. If θ=7 radian, then : (a)l+m>0 (b) l+m<0 (c) l+m=0 (d) nothing can be said
View SolutionIf both roots of the quadratic equation ax2+x+b−a=0 are non real and b>−1, then which of the following is/are correct ? (a) a>0 (b) a<b (c) 3a>2+4b (d) 3a<2+4b
View SolutionIn isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that :
(i) AC>AD
(ii) AE>AC
(iii) AE>AD
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q, and the outer shell has charge +4q. (K=(1)/(4piepsilon_(0)))

Find the electric field in terms of q and the distance r from the common centre of the two shells for (i) b<r<c (ii) c<r<d
View SolutionThe function f(x)=sin3x−msinx is defined on open interval (−π2,π2) and if assumes only 1 maximum value and only 1 minimum value on this interval. Then, which one of the must be correct? (a) 0<m<3 (b) −3<m<0 (c) m>3 (d) m<−3
View SolutionIn the figure shown S is the saurce of white light kept at a distance x0 frorn the plane of the slits. The source moves with a constant specd u towards the slits on the line perpendicular to the plane of the slits and passing through the slit S1. Find the instanteneous velocity (magnituce and direction). of the central maxima at time t having range 0≤t<<x0−du. Assume that D>>d.

View Solution