A conducting loop is held stationary normal to the field between the NS poles of a fixed permanenet magnet. By choosing a magnet sufficiently strong, can we hope to generate current in the loop?
To determine whether a stationary conducting loop placed in a fixed magnetic field can generate current, we can analyze the situation step by step.
1. Understanding the Setup:
- We have a conducting loop positioned between the north (N) and south (S) poles of a permanent magnet. The loop is held stationary and is oriented normal (perpendicular) to the magnetic field lines.
2. Magnetic Field Representation:
- The magnetic field lines between the N and S poles of the magnet are straight and uniform. We can visualize the magnetic field lines running from the north pole to the south pole.
3. Magnetic Flux Concept:
- Magnetic flux (Φ) through the loop is defined as the product of the magnetic field (B) and the area (A) of the loop perpendicular to the field:
Φ=B⋅A⋅cos(θ)
- In this case, since the loop is normal to the field, θ=0 degrees, and thus cos(θ)=1.
4. Stationary Loop:
- Since the loop is stationary, the magnetic field (B) is constant, and the area (A) of the loop does not change. Therefore, the magnetic flux through the loop remains constant over time.
5. Faraday's Law of Electromagnetic Induction:
- According to Faraday's law, the electromotive force (emf) induced in a loop is proportional to the rate of change of magnetic flux through the loop:
emf=−dΦdt
- Since there is no change in magnetic flux (dΦ/dt = 0) because the loop is stationary and the magnetic field is constant, the induced emf is zero.
6. Conclusion on Current Generation:
- If there is no induced emf, there will be no current generated in the loop. Therefore, regardless of how strong the magnetic field is, if the loop does not move or change its orientation, no current will be produced.
Final Answer:
No, we cannot generate current in the loop as it is stationary in a fixed magnetic field, leading to no change in magnetic flux and hence no induced emf.
- We have a conducting loop positioned between the north (N) and south (S) poles of a permanent magnet. The loop is held stationary and is oriented normal (perpendicular) to the magnetic field lines.
- The magnetic field lines between the N and S poles of the magnet are straight and uniform. We can visualize the magnetic field lines running from the north pole to the south pole.
- Magnetic flux (Φ) through the loop is defined as the product of the magnetic field (B) and the area (A) of the loop perpendicular to the field:
Φ=B⋅A⋅cos(θ)
- In this case, since the loop is normal to the field, θ=0 degrees, and thus cos(θ)=1.
- Since the loop is stationary, the magnetic field (B) is constant, and the area (A) of the loop does not change. Therefore, the magnetic flux through the loop remains constant over time.
- According to Faraday's law, the electromotive force (emf) induced in a loop is proportional to the rate of change of magnetic flux through the loop:
emf=−dΦdt
- Since there is no change in magnetic flux (dΦ/dt = 0) because the loop is stationary and the magnetic field is constant, the induced emf is zero.
- If there is no induced emf, there will be no current generated in the loop. Therefore, regardless of how strong the magnetic field is, if the loop does not move or change its orientation, no current will be produced.
No, we cannot generate current in the loop as it is stationary in a fixed magnetic field, leading to no change in magnetic flux and hence no induced emf.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise (Very Short Answer Questions)
33 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problems (Level-I)
28 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise (Long Answer Questions)
1 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
(a) A closed loop is held stationary in the magnetic field between the north and south poles of two permanent magnets held fixed. Can we hope to generate current in the loop by using very strong magnets?
(b) A closed loop moves normal to the constant electric field between the plates of a large capacitor. Is a current induced in the loop (i) when it is wholly inside the region between the capacitor plates (ii) when it is partially outside the plates of the capacitor? The electric field is normal to the plane of the loop.
(c) A rectangular loop and a circular loop are moving out of a uniform magnetic field region (Fig. 6.8) to a field-free region with a constant velocity v. In which loop do you expect the induced emf to be constant during the passage out of the field region? The field is normal to the loops.

(d) Predict the polarity of the capacitor in the situation described by Fig. 6.9.

View SolutionA current loop in a magnetic field
View SolutionA rectangular loop of sides 10 cm and 5 cm with a cut is stationary between the pole pieces of an electromagnet.
The magnetic field of the magnet is normal to the loop. The current feeding the electromagnet is reduced, so that the field decreased from its initial value of 0.2 T at the rate of 0.02Ω. If the cut is joined and the loop has a resistance of 2.0Ω, then the power dissipated by the loop as heat is
View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to
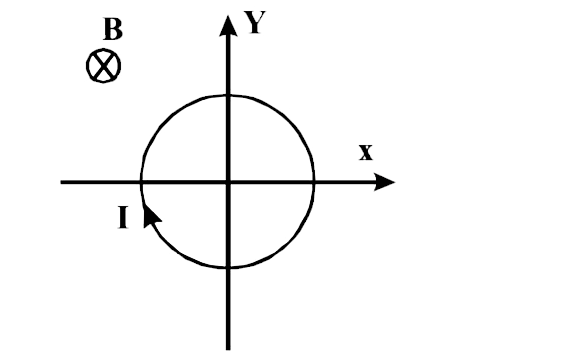
View SolutionA current carrying loop in a uniform magnetic field will experience
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View SolutionA conducting loop confined in a plane is rotated in its own plane with some angular velocity.A uniform and constant magnetic field exist in the region.Find the current induced in the loop.
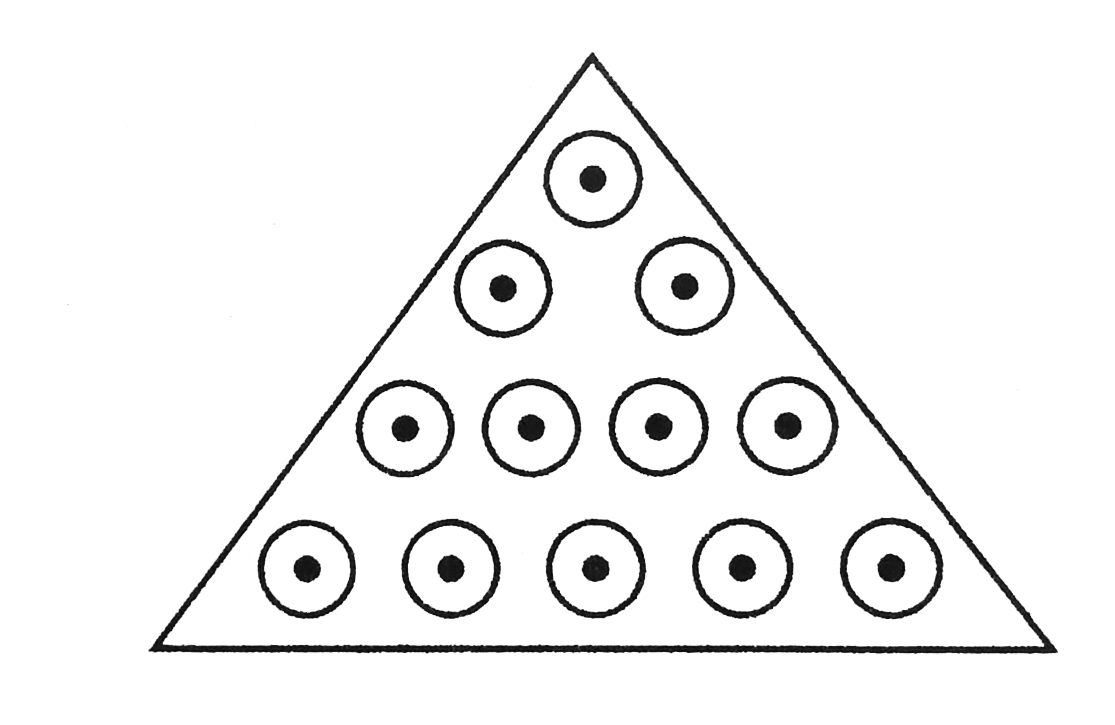
View SolutionA triangular loop is placed in a dot ⊙ magnetic field as shown in figure. Find the direction of induced current in the loop if magnetic field is increasing.
View SolutionA closed loop moves normal to a constant electric field between the plates of capacitor with plane of loop is normal to the field. When the loop is partially outside the plates of capacitor, the induced current in the loop
View SolutionShows a conducting square loop placed parallel to the pole faces of a ring magnet. The pole faces have an area of 1cm^2 each and the field between the poles is 0.10 T. The wires making the loop are all outside the magnetic field. If the magnet is removed in 1.0 s, what is the average emf induced in the loop?

View Solution
