Two concentric circular coils, one of small radius r1 and the other of large radius r2, such that r1>>r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
Suppose a current I2 flows through the outer circular coil. The field at the centre of the coil is
B2=μ0I22r2
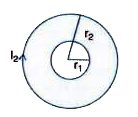
The second co-axially placed coil has very small radius. So B2 may be considered constant over its cross-sectional area
Now, ϕ1=πr21B2=πr21(μ0I22r2)
or ϕ1=μ0πr212r2I2
Comparing with ϕ=M12I2, we get
M12=μ0πr212r2
Also, M21=M12=μ0πr212r2
It would have been difficult to calculate the flux through the bigger coil of the non-uniform field due to the current in the smaller coil and hence the mutual inductance M12. The equality M12=M21 is helpul. Note also that mutual inductance depends solely on the geometry.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise (Long Answer Questions)
1 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise (Short Answer Questions)
21 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE EXERCISE (SELF INDUCTANCE AND MUTUAL INDUCTANCE)
12 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
Two circular coils, one of smaller radius r1 and the other of very large radius r2 are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo concentric circular coils of radius r and R are placed coaxially with centres coinciding If R>>r then calculate the mutual inductance the coils.
View Solution
Knowledge Check
The conducting circular loops of radii R1andR2 are placed in the same plane with their centres coinciding. If R1>>R2, the mutual inductance M between them will be directly proportional to
AR1R2BR2R1CR21R2DR22R1The conducting circular loops of radii R1andR2 are placed in the same plane with their centres coinciding. If R1>>R2, the mutual inductance M between them will be directly proportional to
AR1R2BR2R1CR21R2DR22R1
Two conducting circular loops of radii R1andR2 are placed in the same plane with their centres coincidingt. Find the mutual inductane between them assuming R2<<R1.
View SolutionA small coil of radius r is placed at the centre of a large coil of radius R, where R>>r. The two coils are coplanar. The mutual inductance between the coils is proportional to
View SolutionA long straight wire is placed along the axis of a circuit ring of radius R. The mutual inductance of this system is
View SolutionA coil of radius r is placed at the centre of the large coil of radius R where R⟩r and coils are in same plane.The coefficient of mutual inductance between the coil is
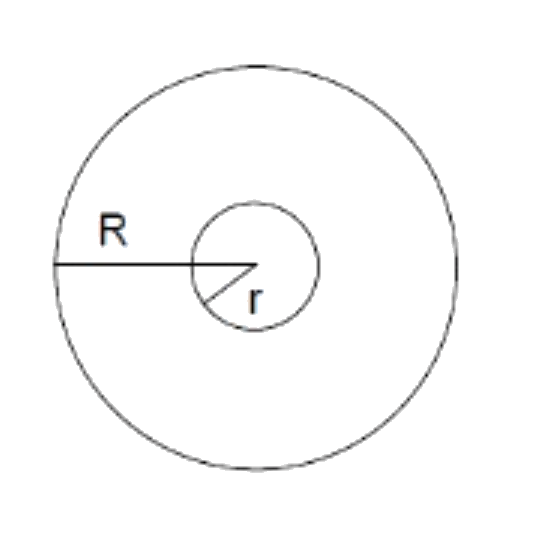
View SolutionTwo concentric co - planar circular loops of radius R and r(<<R) are placed as shown in the figure. The mutual inductance of the system will be
View SolutionThe conducting circular loops of radii R1andR2 are placed in the same plane with their centres coinciding. If R1>>R2, the mutual inductance M between them will be directly proportional to
View Solution
