A current I flows through an infinitly long wire having infinite brands as shown. The radius of the first curved section is a and the radii of the successive curved portions each increases by a factor η. Find magnetic field at O.

The magnetic field at O due to arc AB is B1=μ0iθ4πa⊙ The field at O due to arc CD and other arcs are B2=μ0iθ4πηa,B3=μ04πiθη2a ,………. Etc
Therefore resultant field is B=B1+B2+.......
B=μ0i4πa[1−1η+1η2−1η3......]
The resultant field is the sum of above fields which is a geometric progression with common ratio −1η
Therefore resultant field is B=(μ0iθ4πa)(1+1η)=μ0iθη4πa(η+1)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA
142 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
A current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
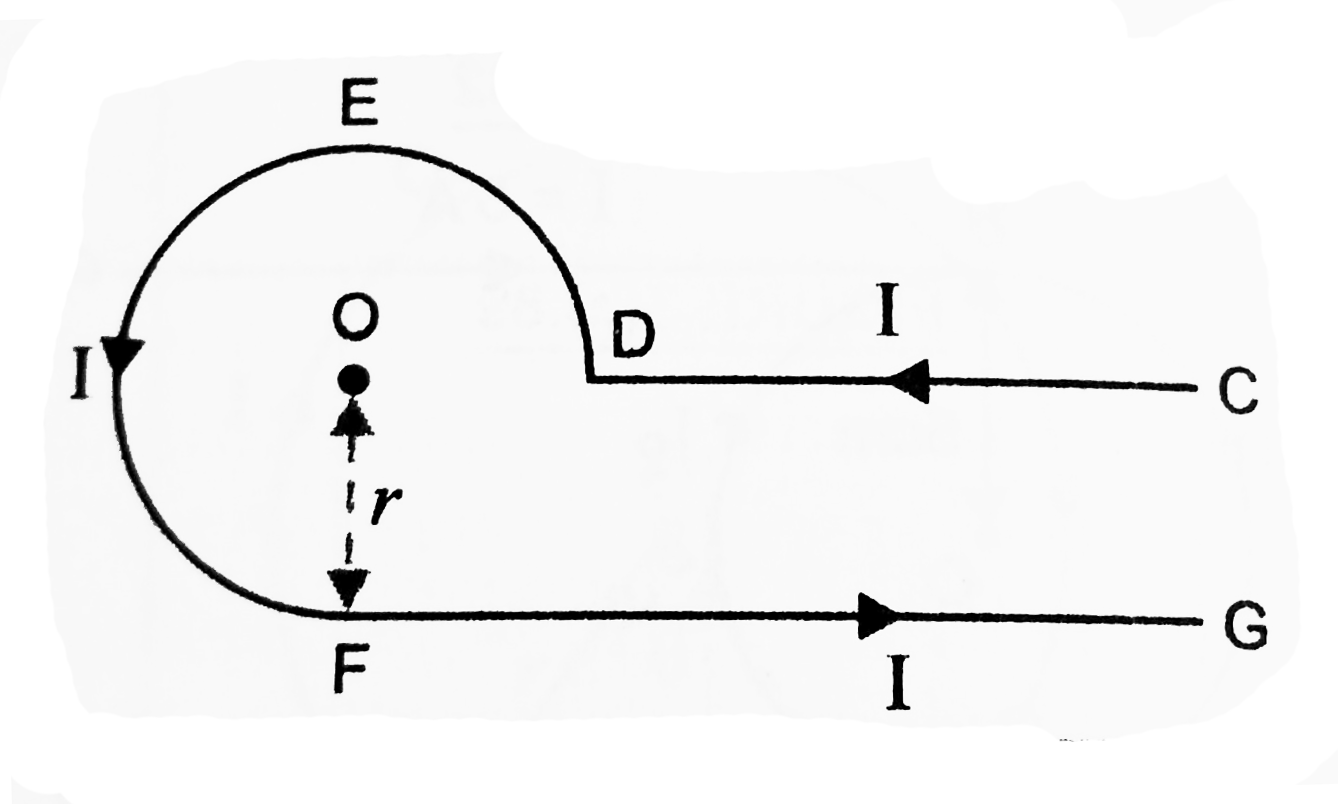
View SolutionA current I is flowing in a conductor shaped as shown in figure. The radius of the curved part is r and length of straight portion is very large. Find the magnetic field induction at the centre O.
View SolutionA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is

View SolutionAn electric current I flows through an infinitely long conductor as shown in Figure 2(a) below. Write an expression and direction for the magnetic field at point P.

View SolutionA current of I amperes is flowing through each of the bent wires as shown. Find the magnitude of magnetic field at O.
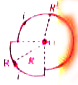
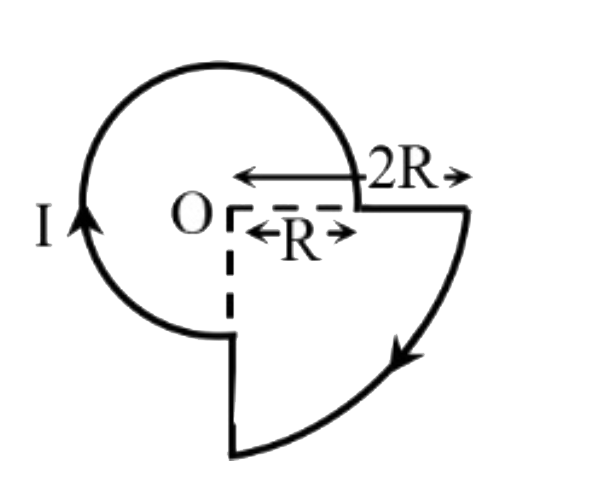
View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
View SolutionMagnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
View Solution
A long wire bent as shown in the figure carries current I=10A. If the radius of the semicircular portion is 1 m, the magnetic induction (in μT) at the center C is
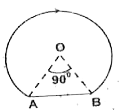
View SolutionTwo very long wires carrying equal current i are bent and arranged as shown in figure. Both AB and CD are arcs of the same circle, both subtending right angles at the centre O. The magnetic field at O is:

View SolutionAn equilateral triangular frame with side a carrying a current I is placed at a distance a from an infinitely long straight wire carrying a current I as shown in the figure. One side of the frame isparallel to the wire. The whole system lies in the xy-plane. Find the magnetic force F acting on the frame.
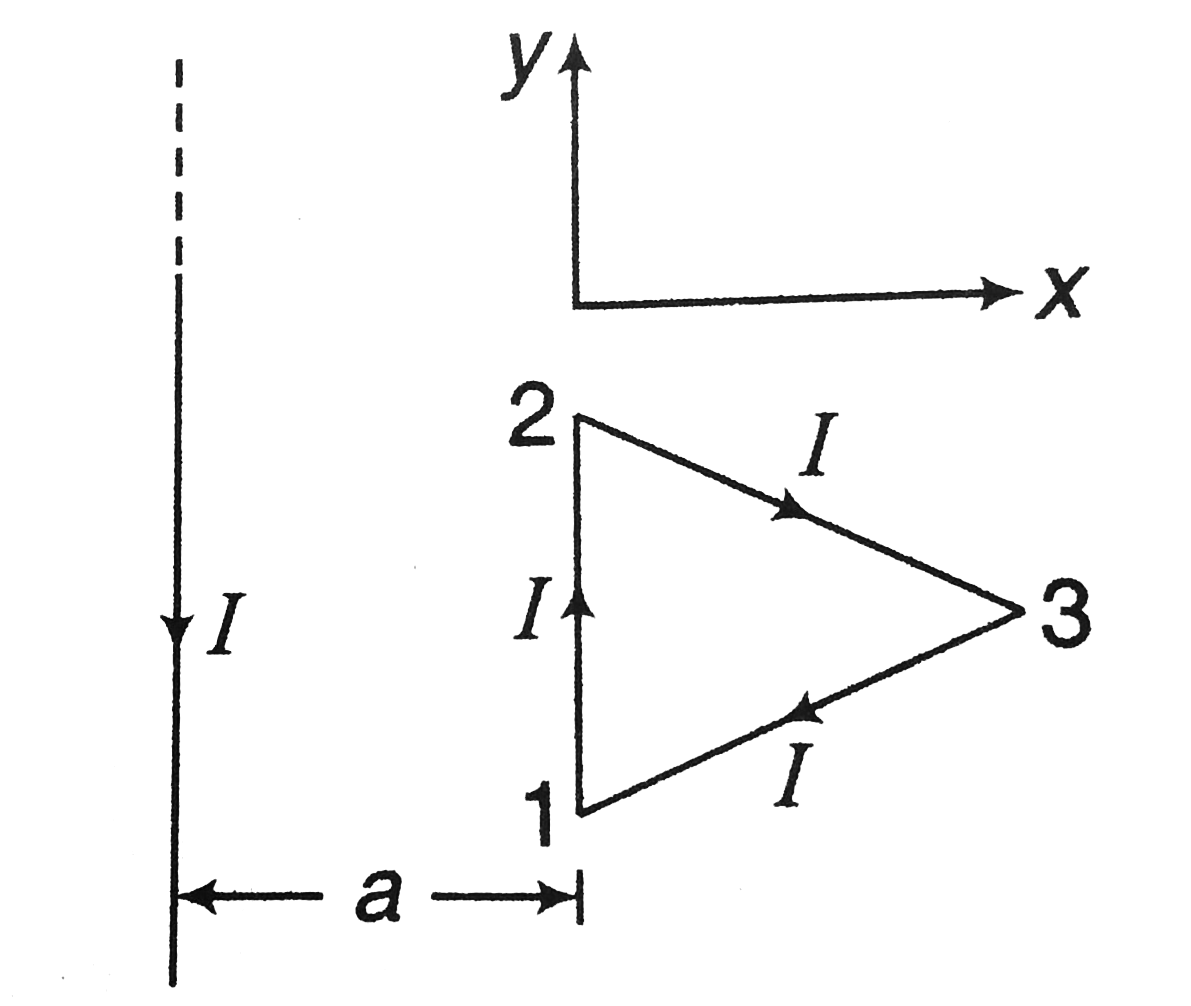
View Solution
