An ionized gas contains both +ve and -ve ions which are initially at rest. The gas is subjected to →E toward positive x-axis, magnetic field along +ve z axis. Then.find the direction of deflection of
a) +ve charged ions b) -ve charged ions
To solve the problem, we need to analyze the motion of both positive and negative ions in the presence of an electric field (E) and a magnetic field (B).
1. Identify the Fields and Their Directions:
- The electric field →E is directed along the positive x-axis.
- The magnetic field →B is directed along the positive z-axis.
2. Determine the Force on Positive Ions:
- For positive ions, the force due to the electric field →FE is given by:
→FE=q→E
where q is the charge of the positive ion.
- Since →E is in the positive x-direction, the force →FE will also be in the positive x-direction.
- The velocity →v of the positive ions will also be in the positive x-direction due to the electric field.
3. Calculate the Magnetic Force on Positive Ions:
- The magnetic force →FB on a charged particle moving in a magnetic field is given by:
→FB=q(→v×→B)
- Here, →v is in the positive x-direction and →B is in the positive z-direction.
- Using the right-hand rule for the cross product:
→v×→B=^i×^k=−^j
- Therefore, the magnetic force →FB on the positive ions is directed in the negative y-direction.
4. Determine the Total Force on Positive Ions:
- The total force →F acting on the positive ions is the sum of the electric and magnetic forces:
→F=→FE+→FB
- Since →FE is in the positive x-direction and →FB is in the negative y-direction, the positive ions will deflect in the negative y-direction.
5. Determine the Force on Negative Ions:
- For negative ions, the force due to the electric field →FE is still given by:
→FE=q→E
- However, since the charge is negative, the force will be in the opposite direction to the electric field, which means it will be in the negative x-direction.
- The velocity →v of the negative ions will be in the negative x-direction.
6. Calculate the Magnetic Force on Negative Ions:
- The magnetic force →FB for the negative ions is:
→FB=q(→v×→B)
- Here, →v is in the negative x-direction and →B is in the positive z-direction.
- Using the right-hand rule:
→v×→B=−^i×^k=^j
- Therefore, the magnetic force →FB on the negative ions is directed in the positive y-direction.
7. Determine the Total Force on Negative Ions:
- The total force →F acting on the negative ions is:
→F=→FE+→FB
- Since →FE is in the negative x-direction and →FB is in the positive y-direction, the negative ions will deflect in the positive y-direction.
Final Results:
- a) The direction of deflection of positive charged ions is negative y-direction.
- b) The direction of deflection of negative charged ions is positive y-direction.
- The electric field →E is directed along the positive x-axis.
- The magnetic field →B is directed along the positive z-axis.
- For positive ions, the force due to the electric field →FE is given by:
→FE=q→E
where q is the charge of the positive ion.
- Since →E is in the positive x-direction, the force →FE will also be in the positive x-direction.
- The velocity →v of the positive ions will also be in the positive x-direction due to the electric field.
- The magnetic force →FB on a charged particle moving in a magnetic field is given by:
→FB=q(→v×→B)
- Here, →v is in the positive x-direction and →B is in the positive z-direction.
- Using the right-hand rule for the cross product:
→v×→B=^i×^k=−^j
- Therefore, the magnetic force →FB on the positive ions is directed in the negative y-direction.
- The total force →F acting on the positive ions is the sum of the electric and magnetic forces:
→F=→FE+→FB
- Since →FE is in the positive x-direction and →FB is in the negative y-direction, the positive ions will deflect in the negative y-direction.
- For negative ions, the force due to the electric field →FE is still given by:
→FE=q→E
- However, since the charge is negative, the force will be in the opposite direction to the electric field, which means it will be in the negative x-direction.
- The velocity →v of the negative ions will be in the negative x-direction.
- The magnetic force →FB for the negative ions is:
→FB=q(→v×→B)
- Here, →v is in the negative x-direction and →B is in the positive z-direction.
- Using the right-hand rule:
→v×→B=−^i×^k=^j
- Therefore, the magnetic force →FB on the negative ions is directed in the positive y-direction.
- The total force →F acting on the negative ions is:
→F=→FE+→FB
- Since →FE is in the negative x-direction and →FB is in the positive y-direction, the negative ions will deflect in the positive y-direction.
- a) The direction of deflection of positive charged ions is negative y-direction.
- b) The direction of deflection of negative charged ions is positive y-direction.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA
142 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
An ionized gas contains both positive and negative ions . If it is subjected simultaneously to an electric field along the +x - direction and a magnetic field along the +y - direction and the negative ions towardws −y - direction
View SolutionPositive and negative ions are productid at the origin. If they are subjected simultaneously to an electric field along the +y−directionandmaGNeticfieldalong+z-direction, then
View SolutionIn a system of particles 8kg mass is subjected to a force of 16N along + ve x-axis and another 8kg mass is subjected to a force of 8N along + ve y-axis. The magnitude of acceleration of centre of mass and the angle made by it with x-axis are given, respectively, by
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionA charge of2.0μC moves with a speed of 2.0X106ms−1 along the positive x-axis. A magnetic field →B of strength (0.20→J+0.40→k)T exists in space. Find the magnetic force acting on the charge
View SolutionA conducting rod AB moves parallel to the x-axis (see Fig.) in a uniform magnetic field pointing in the positive z-direction. The end A of the rod gets positively charged.
 .
.
View SolutionA insulated square frame ABCD of side a is able to rotate about one of its side taken as positive z-axis. A magnetic field B is present in the region given by →B=B0ˆj. A small block of mass m and charge q movable along side CB is initially near C, when frame lies in x−z plane. Now, frame is rotated by constant angular velocity ω about z-axis. Whole system lies in gravity free space. If after time t block reaches point B, find B0 in terms of t.

View SolutionIf the magnetic field is parallel to the positive y-axis and the charged particle is moving along the positive x-axis (Fig.), which way would the Lorentz force be for (a) an electron (negative charge), (b) a proton (positive charge).
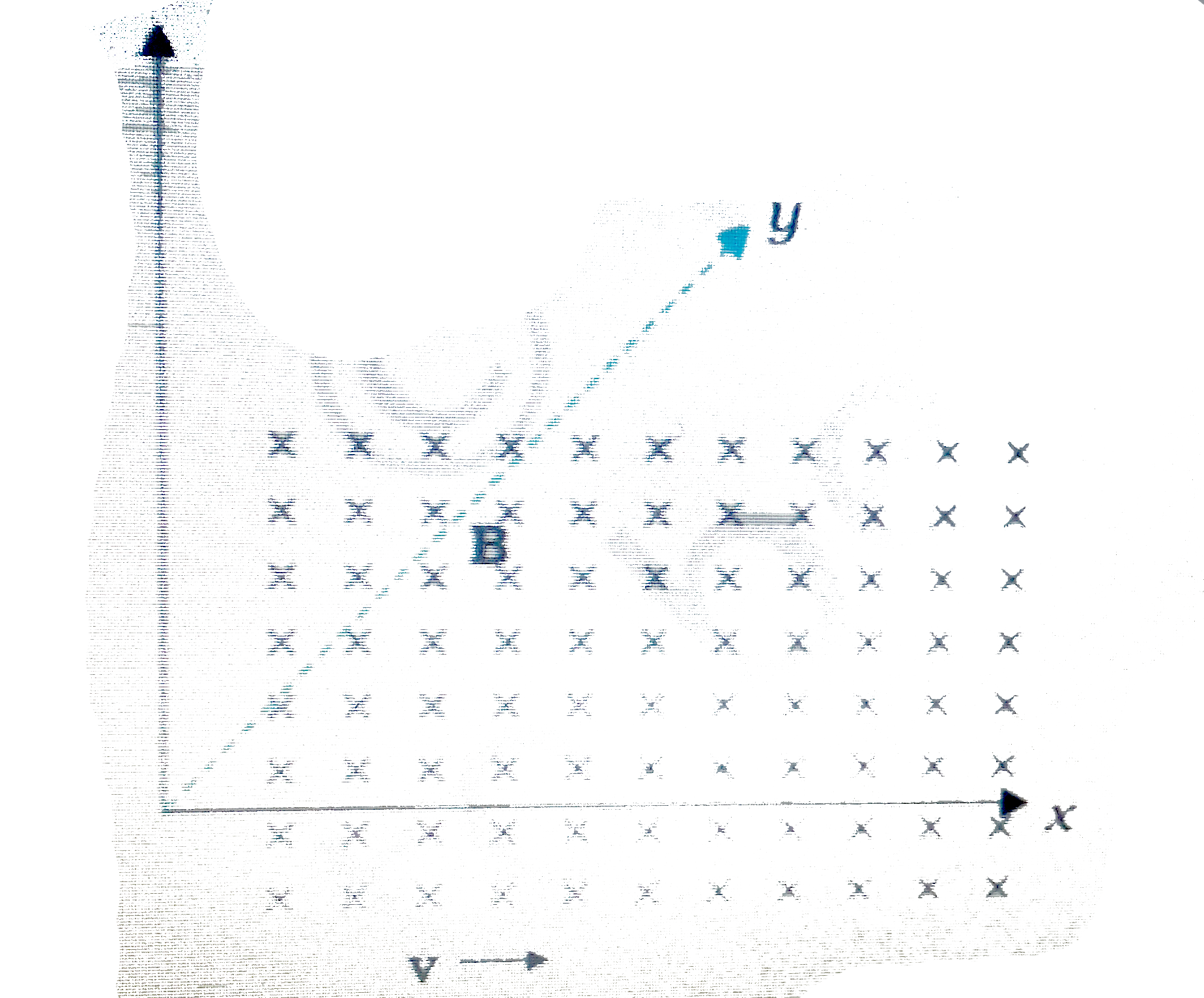
View SolutionAn electron having a charged e moves with a velcoity v in postive x direction. A magnetic field acts on it in positive y direction. The force on the electron acts in (where outward direction is taken as positive z-axis)
View SolutionA moving charged particle q travelling along the positive X-axis enters a uniform magnetic field B. When will the force acting on q be maximum?
View Solution
