On the opposite sides of a wide vertical vessel filled with water, two identical holes are opened, each having cross section area a. The height difference between them is equal to h. Find the resultant force of reaction of water flowing out of vessel.
F=2ρgAhd
F−v×dmdt=v×ρadedt=ρav2
Reaction force by the efflux of the vessel.
F=ρav2,v=√2gh=ρa2gh,F=2ρagh
F≠t=ρa2g(h1−h2)=ρa2gΔh
Similar Questions
On the opposite sides of a wide vertical vessel filled with water, two identical holes are opened, each having cross sectiona area a. The height dference between them is equal to h. Find the resultant force of reaction of water flowing out of vessel.
View SolutionOn the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
View SolutionThe water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionThere are two holes one each along the opposite sides of a wide rectangular tank. The cross section of each hole is 0.01m2 and the vertical distance between the holes is one meter. The tank is filled with water. The net force on the tank in newton when water flows out of the holes is (density of water 1000kg/m3)
View SolutionThe side wall of a wide vertical vessel of height h=75cm a narrow slit (vertical) running all the way down to the bottom of the vessel.
The length of the slit is l=50cm and the width is b=1mm. With the slit closed, water is filled to the top. Find the resultant reaction force of water coming out as the slit is opened. brgt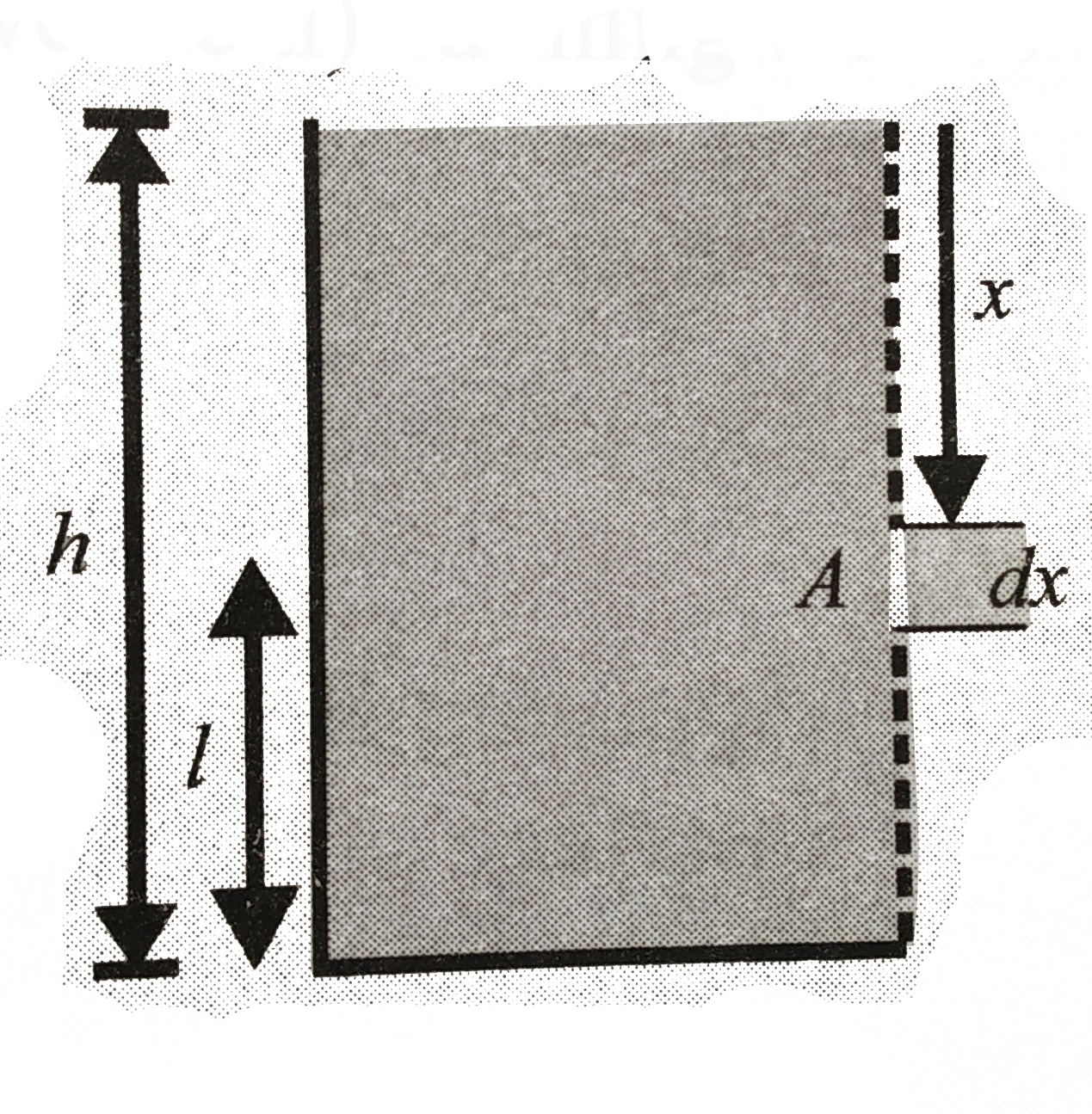
View SolutionWater drains out of a vessel filled with water upto height h through a hole of area A in t seconds.If the height of the water is 4 h then how much time will be required for the water to drain out ?[Assume A<<A0 (area of tank ) ]
View SolutionA cylindrical container of cross-section area, A is filled up with water upto height 'h' Water may exit through a tap of cross sectional area 'a' in the bottom of container. Find out

(a) Velocity of water just after opening of tap.
(b) The area of cross-section of water stream coming out of tape at depth h0 below tap in terms of 'a' just after opening of tap.
(c) Time in which conainer becomes empty.
(Given : (aA)1/2=0.22,h=20cm,h0=20cm
View SolutionA tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
After long time, when the height of water inside the tank again becomes equal to H2, the solid cylinder is taken out. then the velocity of liquid flowing out of the orifice (just after removing the cylinder) will be
View SolutionA fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
View SolutionA vessel in the form of inverted cone. Its height is 8 cm and radius of its top, which is open, is 5 cm. It is filled with water upto the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped in the vessel, one fourth of the water flows out. Find the number of lead shots dropped in the vessel.
View Solution
