P is a point at a distance r from the centre of solid sphere of radius a. The gravitational potential at P is V. IF V is plotted as a function of r, which is the correct curve ?
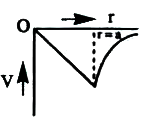
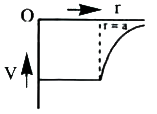
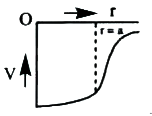
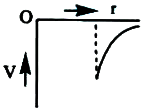
The correct Answer is:C
To determine the correct curve for the gravitational potential V as a function of the distance r from the center of a solid sphere of radius a, we will analyze the gravitational potential both inside and outside the sphere.
Step 1: Understanding Gravitational Potential Inside the Sphere
For a point P located at a distance r (where r<a) from the center of a solid sphere, the gravitational potential V is given by the formula:
V=−GMR+constant
Where M is the mass of the sphere and R is the distance from the center of the sphere to point P.
Step 2: Mass Inside Radius r
The mass m1 of the sphere of radius r can be expressed in terms of the density ρ:
m1=ρ⋅43πr3
The remaining mass of the sphere outside this radius is:
M−m1=M−ρ⋅43πr3
Step 3: Gravitational Potential Inside the Sphere
The gravitational potential inside the sphere can be derived as follows:
V(r)=−G(M−m1a)−Gm1r
Substituting m1:
V(r)=−G⎛⎝M−ρ⋅43πr3a⎞⎠−G⋅ρ⋅43πr3r
This simplifies to:
V(r)=−Gρ⋅4π3(a3−r2⋅r)
Step 4: Gravitational Potential Outside the Sphere
For points outside the sphere (where r>a), the gravitational potential is given by:
V(r)=−GMr
Step 5: Analyzing the Graph
1. For r<a: The potential V varies with r2 and has a parabolic nature.
2. For r>a: The potential V varies inversely with r, which is a hyperbolic nature.
Conclusion
The graph of gravitational potential V as a function of distance r will show a parabolic curve for r<a and will approach a hyperbolic decay for r>a.
Thus, the correct curve to represent V as a function of r is a combination of these two behaviors, typically represented as a continuous curve that transitions from parabolic to hyperbolic.
For a point P located at a distance r (where r<a) from the center of a solid sphere, the gravitational potential V is given by the formula:
The mass m1 of the sphere of radius r can be expressed in terms of the density ρ:
The gravitational potential inside the sphere can be derived as follows:
For points outside the sphere (where r>a), the gravitational potential is given by:
1. For r<a: The potential V varies with r2 and has a parabolic nature.
2. For r>a: The potential V varies inversely with r, which is a hyperbolic nature.
The graph of gravitational potential V as a function of distance r will show a parabolic curve for r<a and will approach a hyperbolic decay for r>a.
Similar Questions
Potential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionTwo spheres one of mass M has radius R. Another sphere has mass 4M and radius 2R. The centre to centre distance between them is 12R. Find the distance from the centre of smaller sphere where
(a) net gravitational field is zero,
(b) net gravitational potential is half the potential on the surface of larger sphere.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the center.
View SolutionAssertion : In moving from centre of a solid sphere to its surface, gravitational potential increases.
Reason : Gravitational field strength increase.
View SolutionA point charge Q is situated (outside) at a distance r from the centre of an uncharged conducting solid sphere of radius R. The potential due to induced charges (on the conductor) at a point B inside the conductor whose distance form the point charge is d is ______
View SolutionThe distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View Solution