Two spherical balls each of mass 1 kg are placed 1 cm apart. The gravitational force of attraction between them - newtons
6.67×10−9
6.67×10−7
6.67×10−8
6.67×10−5
The correct Answer is:B
To find the gravitational force of attraction between two spherical balls each of mass 1 kg and placed 1 cm apart, we can use Newton's law of universal gravitation, which is given by the formula:
F=G⋅m1⋅m2r2
Where:
- F is the gravitational force,
- G is the universal gravitational constant (6.67×10−11N m2/kg2),
- m1 and m2 are the masses of the two objects (in this case, both are 1 kg),
- r is the distance between the centers of the two masses (1 cm, which we need to convert to meters).
1. Identify the values:
- Mass of the first ball, m1=1kg
- Mass of the second ball, m2=1kg
- Distance between the balls, r=1cm=0.01m
- Gravitational constant, G=6.67×10−11N m2/kg2
2. Plug the values into the formula:
F=G⋅m1⋅m2r2
Substituting the values:
F=6.67×10−11⋅1⋅1(0.01)2
3. Calculate r2:
r2=(0.01)2=0.0001m2
4. Substitute r2 back into the equation:
F=6.67×10−110.0001
5. Perform the division:
F=6.67×10−11÷0.0001=6.67×10−11÷10−4=6.67×10−7N
6. Final answer:
The gravitational force of attraction between the two balls is:
F=6.67×10−7N
- F is the gravitational force,
- G is the universal gravitational constant (6.67×10−11N m2/kg2),
- m1 and m2 are the masses of the two objects (in this case, both are 1 kg),
- r is the distance between the centers of the two masses (1 cm, which we need to convert to meters).
- Mass of the first ball, m1=1kg
- Mass of the second ball, m2=1kg
- Distance between the balls, r=1cm=0.01m
- Gravitational constant, G=6.67×10−11N m2/kg2
F=G⋅m1⋅m2r2
Substituting the values:
F=6.67×10−11⋅1⋅1(0.01)2
r2=(0.01)2=0.0001m2
F=6.67×10−110.0001
F=6.67×10−11÷0.0001=6.67×10−11÷10−4=6.67×10−7N
The gravitational force of attraction between the two balls is:
F=6.67×10−7N
Similar Questions
Knowledge Check
Two identical spheres of radius R made of the same material are kept at a distance d apart. Then the gravitational attraction between them is proportional to
Ad−2Bd2Cd4Dd
Two spheres of masses 38 kg and 15 kg each are placed with their centres 20 cm apart. The force of attraction between them is equal to 0.1 milligram wt. Calculate the constant of gravitation.
View SolutionTwo point charges of charge q1 and q2 (both of same sign) and each of mass m are placed such that gravitational attraction between them balances the electrostatic replusion. Are they in stable equilibrium ? If not then what is the nature of equilibrium ?
View SolutionTwo spheres of the same material and same radius r are touching each other. If the gravitational force of attraction between them is directly proportional to rn, then the value of n is :
View SolutionTwo balls, each of radius R, equal mass and density are placed in contact, then the force of gravitation between them is proportional to
View SolutionTwo balls, each of radius R, equal mass and density are placed in contact, then the force of gravitation between them is proportional to
View SolutionTwo identical spherical balls, each of mass m, are placed as shown in figure. Plot the variation of g(gravitation intensity) along the x-axis due to both the masses.
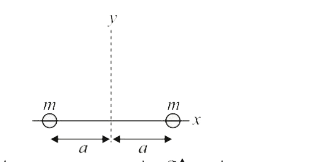
View SolutionIf masses of two point objects are tripled and distance between them is doubled , then gravitational force of attraction between them will
View Solution

