If a planet of mass .m. is revolving around the sun in a circular orbit of radius .r. with time period T, then the mass of the sun is
4π2r3GT
4π2r3GT2
4π2rGT
4π2r3G2T2
The correct Answer is:B
To find the mass of the sun (M) when a planet of mass (m) is revolving around it in a circular orbit of radius (r) with a time period (T), we can use the concepts of gravitational force and centripetal force.
1. Identify the Forces Acting on the Planet:
The planet experiences two main forces:
- The gravitational force (F_g) acting towards the sun.
- The centripetal force (F_c) required to keep the planet in circular motion.
2. Write the Expression for Gravitational Force:
The gravitational force between the sun and the planet is given by Newton's law of gravitation:
Fg=G⋅M⋅mr2
where G is the gravitational constant, M is the mass of the sun, m is the mass of the planet, and r is the radius of the orbit.
3. Write the Expression for Centripetal Force:
The centripetal force required to keep the planet moving in a circular orbit is given by:
Fc=mv2r
where v is the tangential velocity of the planet.
4. Relate Tangential Velocity to Time Period:
The tangential velocity v can be expressed in terms of the time period T:
v=2πrT
Substituting this into the centripetal force equation gives:
Fc=m(2πrT)2r=m⋅4π2rT2
5. Set Gravitational Force Equal to Centripetal Force:
Since the gravitational force provides the necessary centripetal force, we can set these two forces equal to each other:
G⋅M⋅mr2=m⋅4π2rT2
6. Cancel Out the Mass of the Planet:
We can cancel m from both sides (assuming m≠0):
G⋅Mr2=4π2rT2
7. Rearrange to Solve for the Mass of the Sun (M):
Now, we can solve for M:
M=4π2r3GT2
Final Answer:
The mass of the sun is given by:
M=4π2r3GT2
The planet experiences two main forces:
- The gravitational force (F_g) acting towards the sun.
- The centripetal force (F_c) required to keep the planet in circular motion.
The gravitational force between the sun and the planet is given by Newton's law of gravitation:
Fg=G⋅M⋅mr2
where G is the gravitational constant, M is the mass of the sun, m is the mass of the planet, and r is the radius of the orbit.
The centripetal force required to keep the planet moving in a circular orbit is given by:
Fc=mv2r
where v is the tangential velocity of the planet.
The tangential velocity v can be expressed in terms of the time period T:
v=2πrT
Substituting this into the centripetal force equation gives:
Fc=m(2πrT)2r=m⋅4π2rT2
Since the gravitational force provides the necessary centripetal force, we can set these two forces equal to each other:
G⋅M⋅mr2=m⋅4π2rT2
We can cancel m from both sides (assuming m≠0):
G⋅Mr2=4π2rT2
Now, we can solve for M:
M=4π2r3GT2
The mass of the sun is given by:
M=4π2r3GT2
Similar Questions
A small planet is revolving around a massive star in a circular orbit of radius R with a period of revolution T. If the gravitational force between the planet and the star were proportional to R−5/2, then T would be proportional to
View SolutionA small planet is revolving around a massive star in a circular orbit of radius R with a period of revolution T. If the gravitational force between the planet and the star were proportional to R−5/2, then T would be proportional to
View Solution
Knowledge Check
If a planet revolves around the sun in a circular orbit of radius a with a speed of revolution T, then (K being a positive constant
AT=Ka2/3BT=Ka3/2CT=Ka2DT=Ka3A planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the ends of the minor axis and major axis close to the sun is
ATπ2eBT(2eπ−1)CTe2πDT(14−e2π)
Explain the motion of a planet around the sun in a circular path?
View SolutionIf the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, its areal velocity is :
View SolutionMany planets are revolving around the fixed sun in circular orbits of different radius (R) and difference time period (T) To estimate the mass of the sun the orbital radius (R) and time period (T) of planets were noted. Then log10 T v/s log10R curve was plotted.
The curve was found to be approximately straight line (as shown in) having y intercept =6.0 (Neglect the gravitational interaction among the planets) [Take G=203×10−11 in MKS, π2=10]
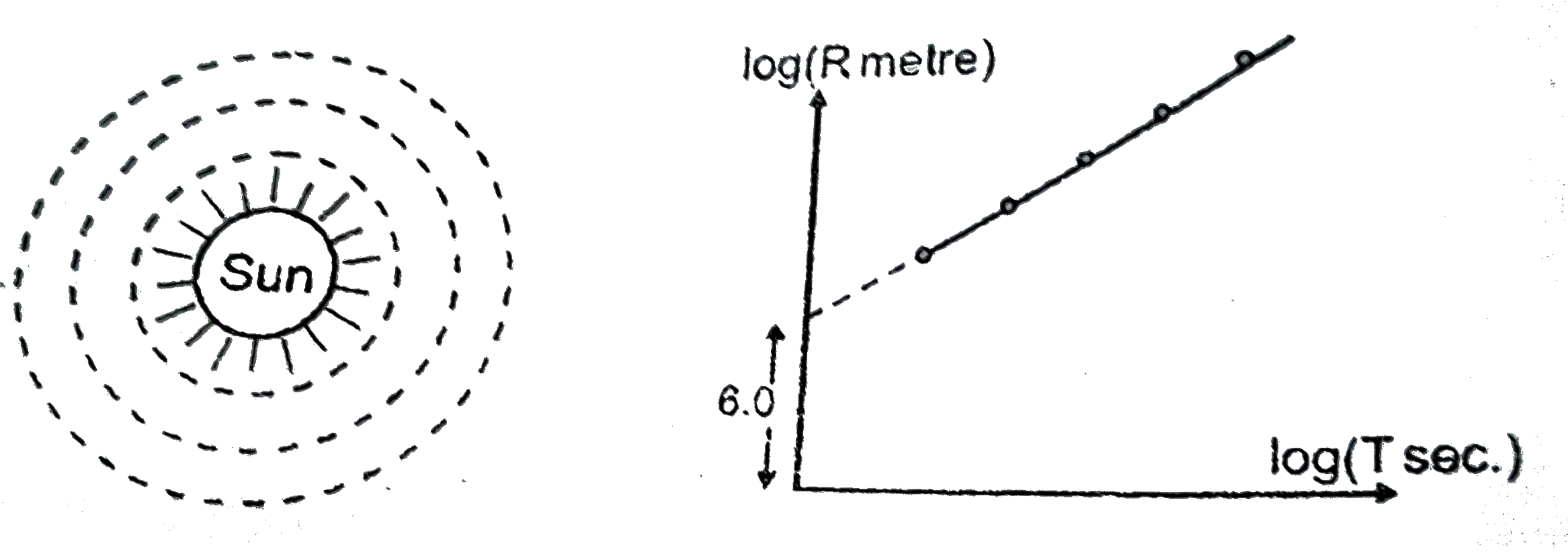
The slope of the line should be .
View SolutionConsider that the Earth is revolving around the Sun in a circular orbit with a period T. The area of the circular orbit is directly proportional to
View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius r with a period of revolution T. On what power of r will the square of time period will depend if the gravitational force of attraction between the planet and the star is proportional to r−5/2.
View Solution
