Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V against r is discontinuous
B. The plot of E against r is discontinuous.
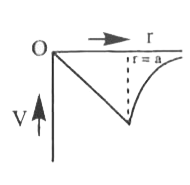
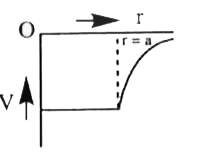

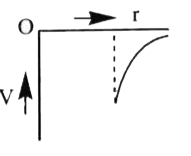
The correct Answer is:C
Step by step video solution for Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements. A. the plot of V against r is discontinuous B. The plot of E against r is discontinuous. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Let V and E be the gravitational potential field. Then select the correct alternative (s)
View SolutionLet V and E be the gravitational potential field. Then select the correct alternative(s) :
View SolutionLet V and E denote the gravitational potential and gravitational field at a point. It is possile to have
View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionWhich graph best represents the variation of electric potential as a function of distance from the centre of a uniformly charged solid sphere of charge of radius R ?

View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View SolutionFollowing curve shows the variation of intesity of gravitational field (→I) with distance from the centre of solid sphere(r) :
View SolutionLet E1andE2 denotes gravitational field at distance r1andr2 from the axis of an infinitely long solid cylinder of the radius R. Which of the following must hold true ?
View SolutionGravitational potential at a distance 'r' from a point mass 'm' is
V=−GMr
Find gravitational field strength at that point.
View Solution
