A planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the ends of the minor axis and major axis close to the sun is
dAdt = constant t ,
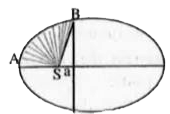
tABT=(Area)SAB(Area) ellipse=πab4−12b(ea)πab
Similar Questions
A planet is revolving around the sun in an elliptical orbit having eccentricity e(=π4). If the time period of revolution is 16 months then find the time taken by the planet in going from A to B in months.
 View Solution
View SolutionA planet revolves around the sun in an elliptical . The linear speed of the planet will be maximum at
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A planet revolves around the sun in an elliptical orbit. If vp and va are the velocities of the planet at the perigee and apogee respectively, then the eccentricity of the elliptical orbit is given by :
AvpvaBva−vpva+vpCvp+vavp−vaDvp−vavp+va - Question 2 - Select One
A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
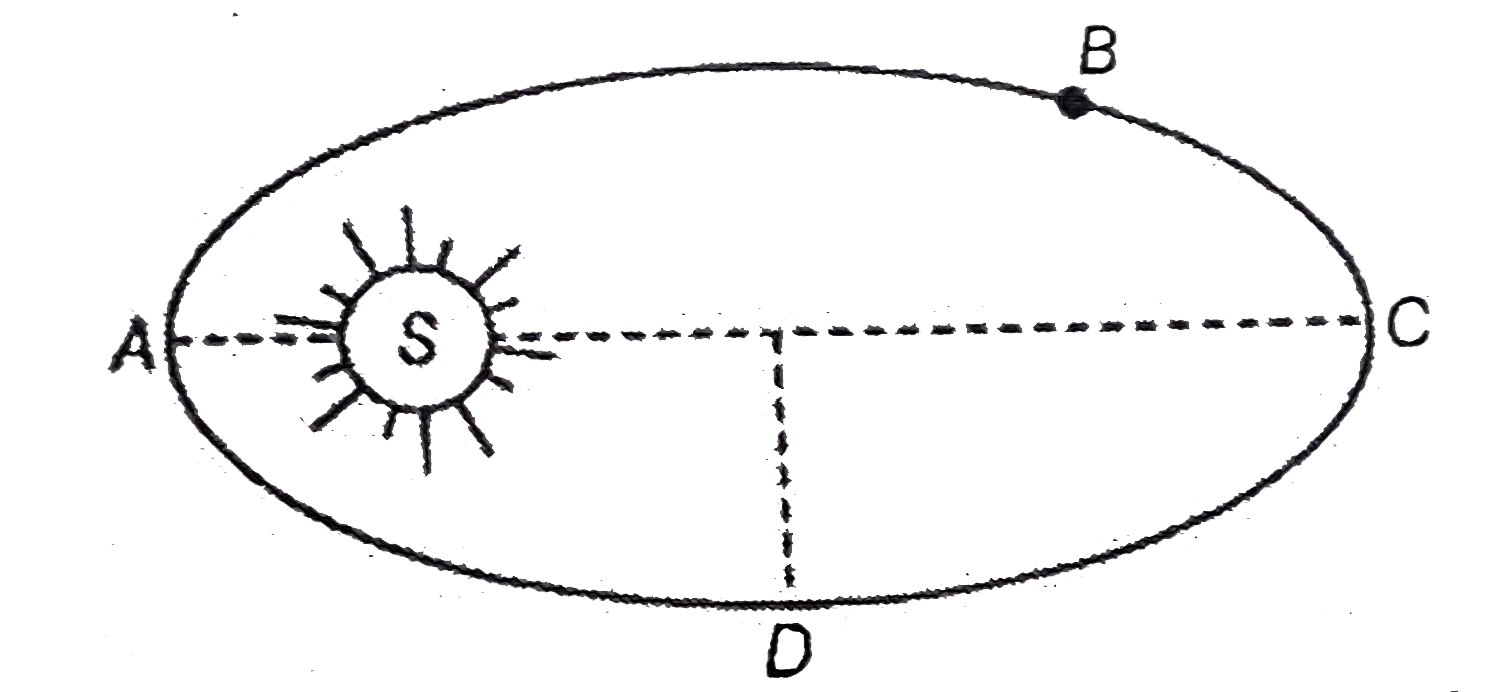 AABBCCDD
AABBCCDD - Question 3 - Select One
A planet revolves around the sun in an elliptical orbit. Suppose that the gravitational attraction between the sun and the planet suddenly disappear then the planet would move
Atowards the sun in a spiral pathBaway from the sun along a straight path with continuously increasing speedCwith constant speed along a tangential path to the oribtDtowards the sun along a straight path with constant speed
A planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
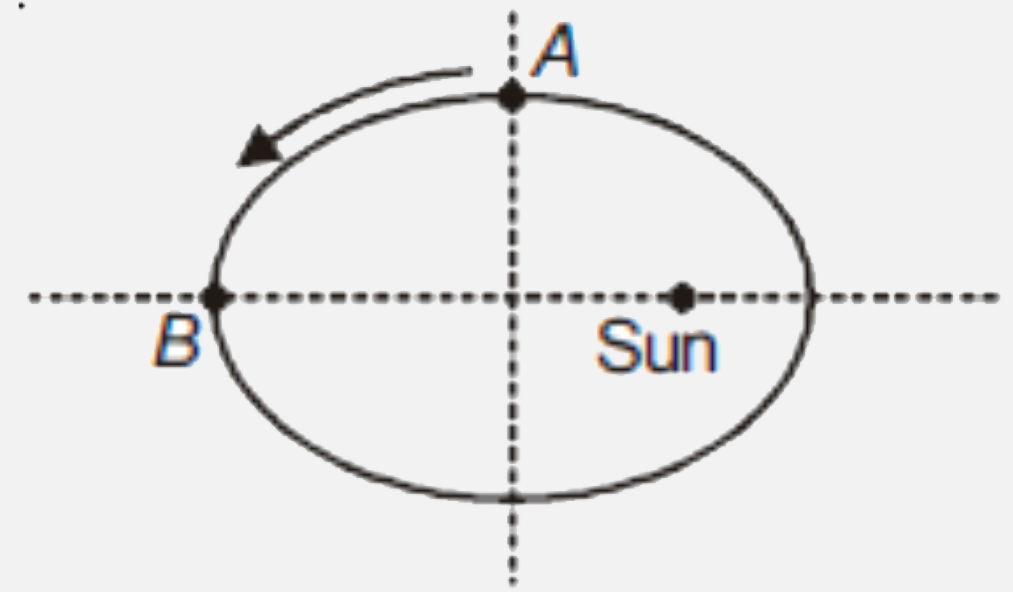
View SolutionA planet is revolving around the sun as shown in elliptical path. The correct option is
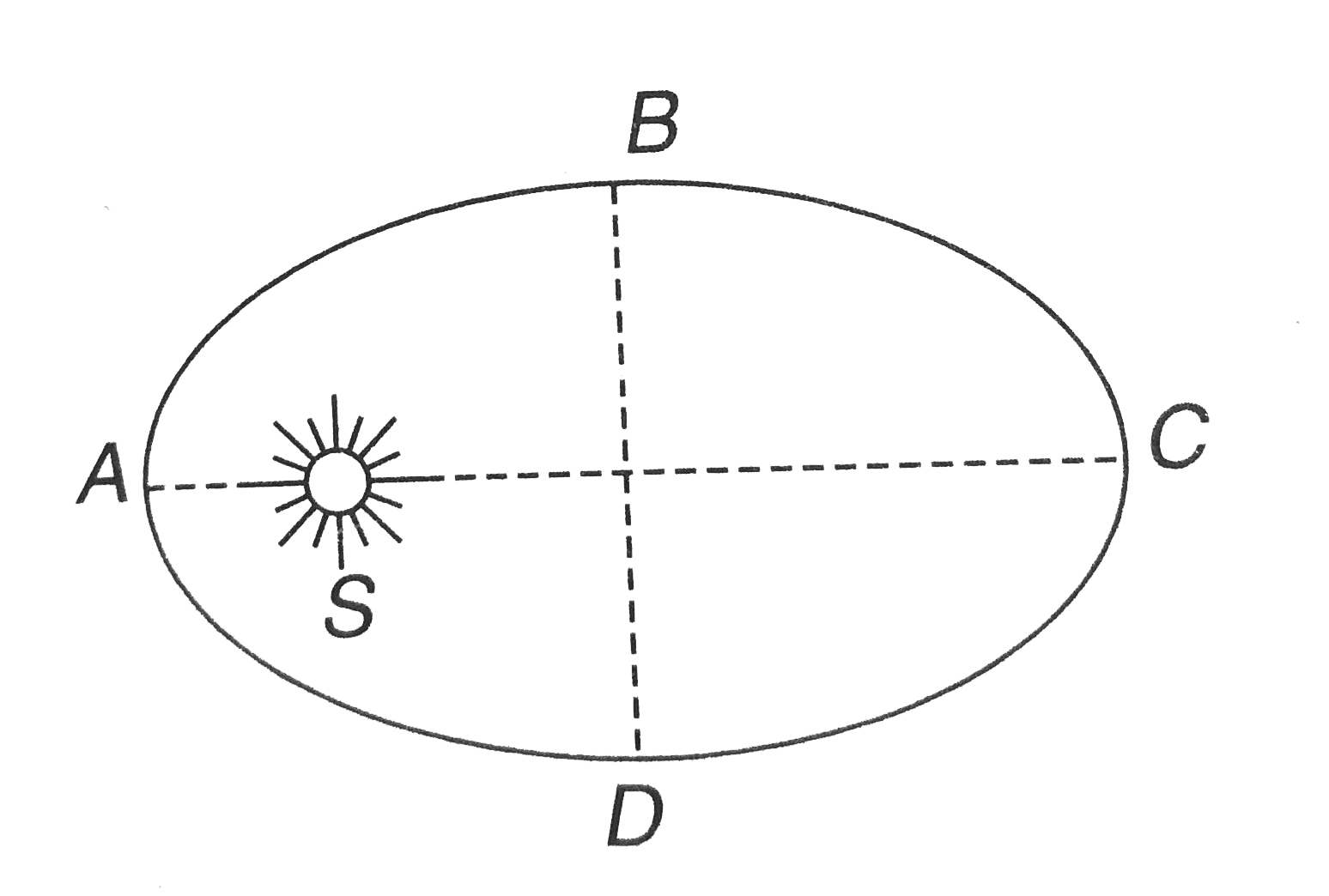 View Solution
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
 View Solution
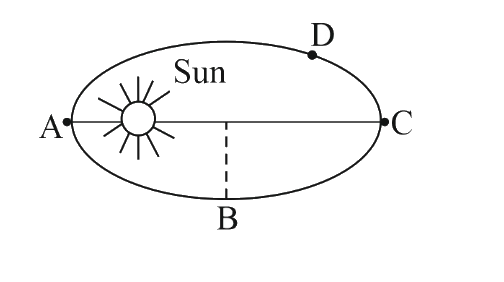
View SolutionA planet is moving round the sun in an elliptical orbit as shows. As the planet moves from A to B
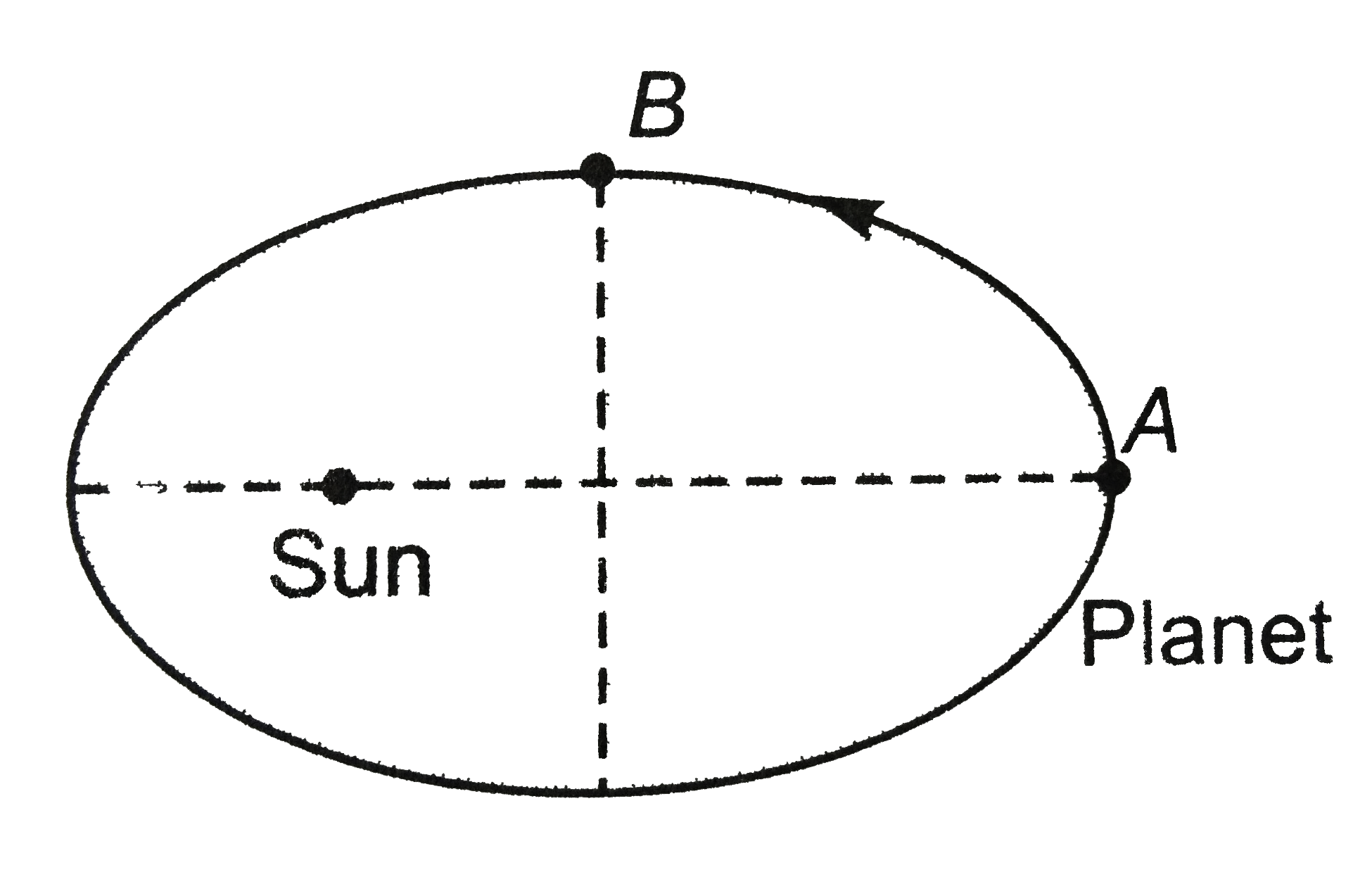 View Solution
View SolutionFor a planet revolving around Sun in an elliptical orbit, to obtain its velocity at any point we have to apply
View Solution
