Find the angle .θ. with the lower vertical at which the resultant acceleration of the bob is along the horizontal, when the perpendicular is released from horizontal position.
To solve the problem of finding the angle θ with the lower vertical at which the resultant acceleration of the bob is horizontal, we will follow these steps:
Step 1: Understand the forces acting on the bob
When the bob is released from the horizontal position, it experiences two types of acceleration:
1. Centripetal acceleration (ac): directed towards the center of the circular path.
2. Tangential acceleration (at): directed along the path of motion.
Step 2: Set up the geometry
Let:
- L be the length of the pendulum.
- θ be the angle with the lower vertical.
- The angle at the point of release from the horizontal is 90∘.
Step 3: Analyze the resultant acceleration
The resultant acceleration of the bob will be horizontal when the vertical component of the acceleration is zero. This means that the vertical component of the acceleration must balance out.
Step 4: Express the components of acceleration
From the geometry:
- The centripetal acceleration ac can be expressed as:
ac=v2L
- The tangential acceleration at is given by:
at=gsinθ
Step 5: Relate the accelerations
For the resultant acceleration to be horizontal, we can write:
sin(90∘−θ)=atac
This simplifies to:
cosθ=gsinθv2L
Step 6: Substitute for v
Using the relationship between v and θ:
v2=2gLcosθ
Substituting this back into the equation gives:
cosθ=gsinθ2gLcosθL=sinθ2cosθ
Step 7: Rearranging the equation
This leads to:
2cos2θ=sinθ
Using the identity sinθ=2sinθcosθ, we can rewrite it as:
2cos2θ−sinθ=0
Step 8: Use the identity sin2θ+cos2θ=1
Substituting sin2θ=1−cos2θ into the equation gives:
2cos2θ−√1−cos2θ=0
Step 9: Solve for θ
After simplifying, we find:
tanθ=12
Thus,
θ=tan−1(12)
Final Answer
The angle θ with the lower vertical at which the resultant acceleration of the bob is horizontal is:
θ=tan−1(√2)
---
When the bob is released from the horizontal position, it experiences two types of acceleration:
1. Centripetal acceleration (ac): directed towards the center of the circular path.
2. Tangential acceleration (at): directed along the path of motion.
Let:
- L be the length of the pendulum.
- θ be the angle with the lower vertical.
- The angle at the point of release from the horizontal is 90∘.
The resultant acceleration of the bob will be horizontal when the vertical component of the acceleration is zero. This means that the vertical component of the acceleration must balance out.
From the geometry:
- The centripetal acceleration ac can be expressed as:
ac=v2L
- The tangential acceleration at is given by:
at=gsinθ
Step 5: Relate the accelerations
For the resultant acceleration to be horizontal, we can write:
sin(90∘−θ)=atac
This simplifies to:
cosθ=gsinθv2L
Using the relationship between v and θ:
v2=2gLcosθ
Substituting this back into the equation gives:
cosθ=gsinθ2gLcosθL=sinθ2cosθ
This leads to:
2cos2θ=sinθ
Using the identity sinθ=2sinθcosθ, we can rewrite it as:
2cos2θ−sinθ=0
Substituting sin2θ=1−cos2θ into the equation gives:
2cos2θ−√1−cos2θ=0
After simplifying, we find:
tanθ=12
Thus,
θ=tan−1(12)
The angle θ with the lower vertical at which the resultant acceleration of the bob is horizontal is:
θ=tan−1(√2)
Similar Questions
A uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
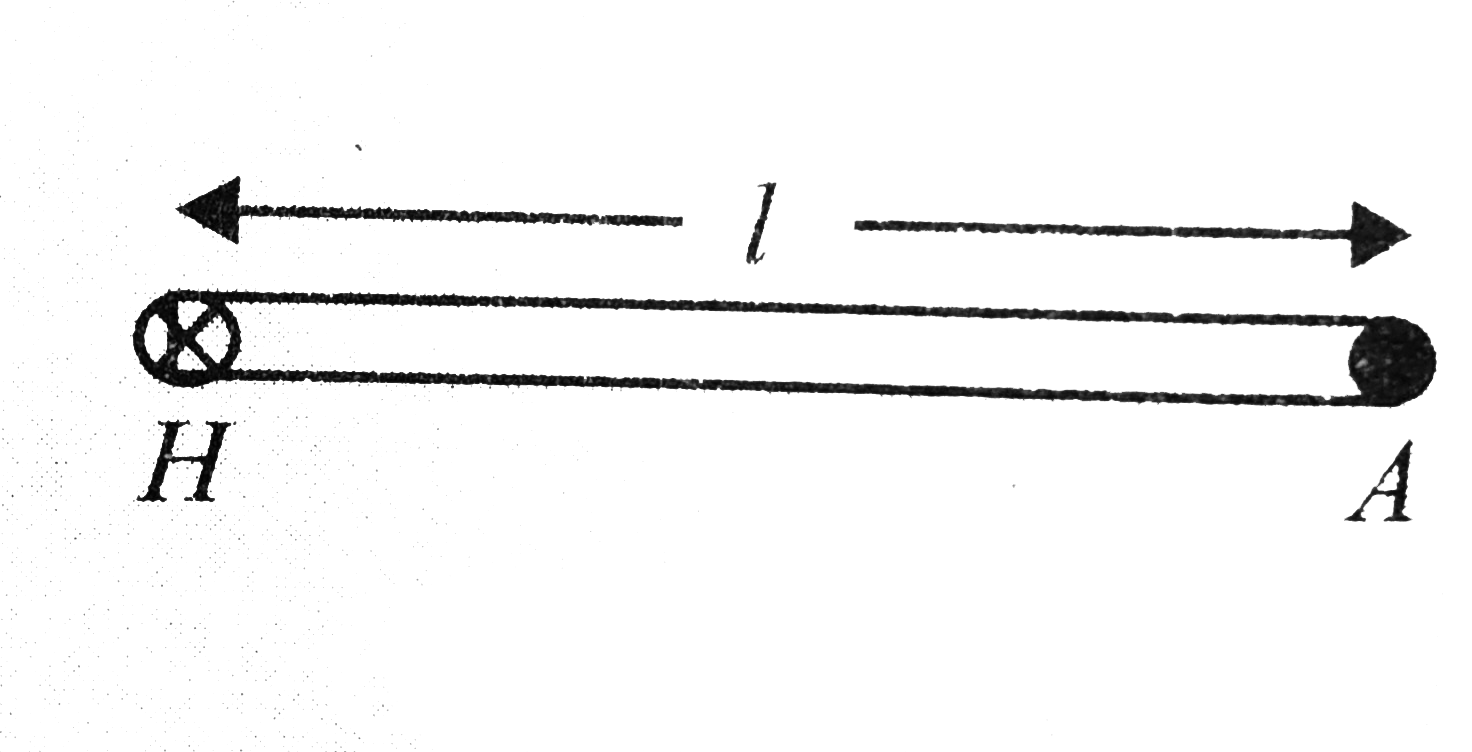
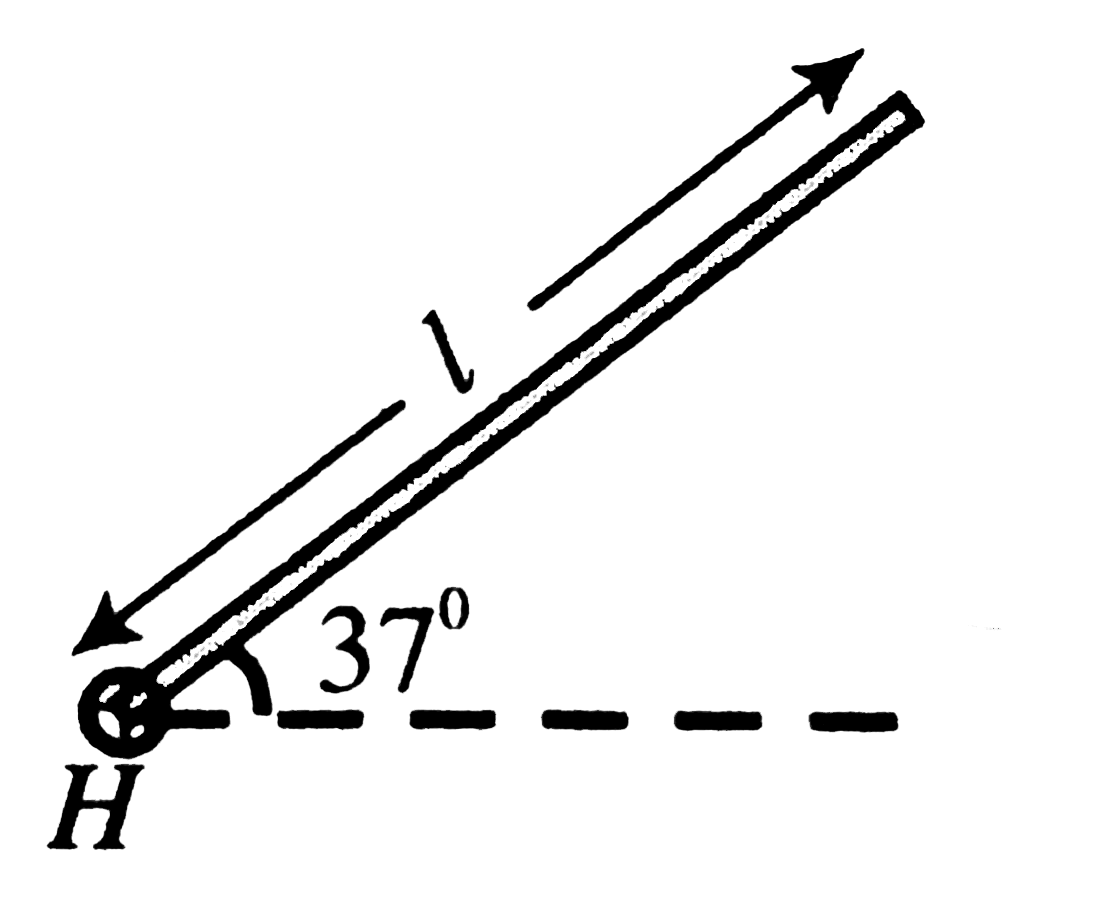
View SolutionA uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hinged at point H. Find angular acceleration α of the rod just after it is released from initial position making an angle of 37∘ with horizontal from rest?
View SolutionA uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at ann angle θ with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?
View Solution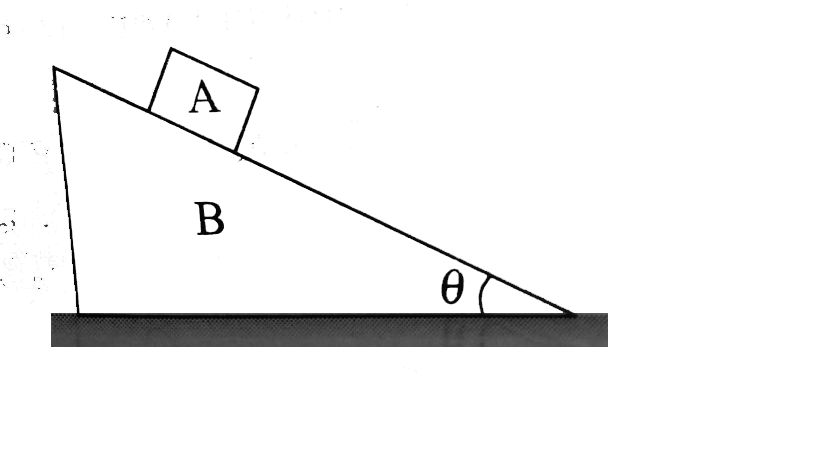
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?
View SolutionIn the figure given in the text if mass of the rod is m then find hinge force.
(a). Just after the rod is released from the horizontal position.
(b). When rod becomes vertical
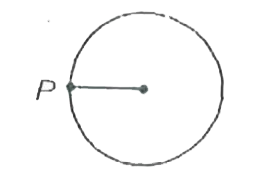
View SolutionA uniform disc of mass m and radius R is pivoted at point P and is free rotate in vertical plane. The centre C of disc is initially in horizontal position with P as shown in figure. If it is released from this position, then its angular acceleration when the line PC is inclined to the horizontal at an angle θ is
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionThe angle which the free surface of a liquid filled in a container will make with horizontal if the container is accelerated horizontally with acceleration g√3 is
View SolutionA disc of a mass M and radius R can rotate freely in vertical plane about a horizontal axis at O. Distant r from the center of disc as shown in the figure. The disc is released from rest in the shown position.

The angular acceleration of disc when OC rotates by an angles of 37∘ is
View SolutionA bob suspended from the ceiling of a car which is accelerating on a horizontal road. The bob stays t rest with respect to the car when the string is making an angle θ with the vertical.The linear momentum of the bob as seen from the road is increasing with momentum? If not, where is the external force which changes the linear momentum?
View Solution