Find the work done in lifting a stone of mass 10 kg and specific gravity 3 from the bed of a lake to a height of 6 m in water.
To find the work done in lifting a stone of mass 10 kg and specific gravity 3 from the bed of a lake to a height of 6 m in water, we can follow these steps:
Step 1: Understand the given data
- Mass of the stone (m) = 10 kg
- Specific gravity (SG) = 3
- Height to lift the stone (h) = 6 m
- Acceleration due to gravity (g) = 9.8 m/s²
Step 2: Calculate the density of the stone
Specific gravity is the ratio of the density of the substance to the density of water. The density of water (ρ_water) is approximately 1000 kg/m³. Therefore, the density of the stone (ρ_stone) can be calculated as:
ρstone=SG×ρwater=3×1000kg/m3=3000kg/m3
Step 3: Calculate the volume of the stone
The volume (V) of the stone can be calculated using the formula:
V=mρstone=10kg3000kg/m3=1300m3
Step 4: Calculate the buoyant force acting on the stone
The buoyant force (F_b) can be calculated using Archimedes' principle:
Fb=ρwater×V×g=1000kg/m3×1300m3×9.8m/s2
Fb=9800300N=32.67N
Step 5: Calculate the weight of the stone
The weight (W) of the stone can be calculated as:
W=m×g=10kg×9.8m/s2=98N
Step 6: Calculate the effective weight to be lifted
The effective weight (W_eff) that needs to be lifted in water is the weight of the stone minus the buoyant force:
Weff=W−Fb=98N−32.67N=65.33N
Step 7: Calculate the work done in lifting the stone
The work done (W_done) in lifting the stone can be calculated using the formula:
Wdone=Weff×h=65.33N×6m=392J
Final Answer
The work done in lifting the stone is 392 Joules.
---
- Mass of the stone (m) = 10 kg
- Specific gravity (SG) = 3
- Height to lift the stone (h) = 6 m
- Acceleration due to gravity (g) = 9.8 m/s²
Specific gravity is the ratio of the density of the substance to the density of water. The density of water (ρ_water) is approximately 1000 kg/m³. Therefore, the density of the stone (ρ_stone) can be calculated as:
ρstone=SG×ρwater=3×1000kg/m3=3000kg/m3
The volume (V) of the stone can be calculated using the formula:
V=mρstone=10kg3000kg/m3=1300m3
The buoyant force (F_b) can be calculated using Archimedes' principle:
Fb=ρwater×V×g=1000kg/m3×1300m3×9.8m/s2
Fb=9800300N=32.67N
The weight (W) of the stone can be calculated as:
W=m×g=10kg×9.8m/s2=98N
The effective weight (W_eff) that needs to be lifted in water is the weight of the stone minus the buoyant force:
Weff=W−Fb=98N−32.67N=65.33N
The work done (W_done) in lifting the stone can be calculated using the formula:
Wdone=Weff×h=65.33N×6m=392J
The work done in lifting the stone is 392 Joules.
Similar Questions
What is the work done in taking an object of mass 1kg from the surface of the earth to a height equal to the radius of the earth ?
(G=6.67×10−11Nm2/Kg2, Radius of the earth = 6400 km, Mass of the earth =6×1024kg.)
View SolutionFind work done in shifting a body of mass m from a height h above the earth's surface to a height 2h above the earth's surface..
View Solution
Knowledge Check
If a body of mass 5 kg is lifted from the ground level to a height of 5m then ratio of its inertia is …………..
A1:1BsameCconstantDnot defined
The work that must be done in lifting a body of weight P from the surface of the earth to a height h is
View SolutionIf the acceleration due to gravity at the surface of the earth is g, the work done in slowly lifting a body ofmass m from the earth's surface to a height R equal to the radius of the earth is
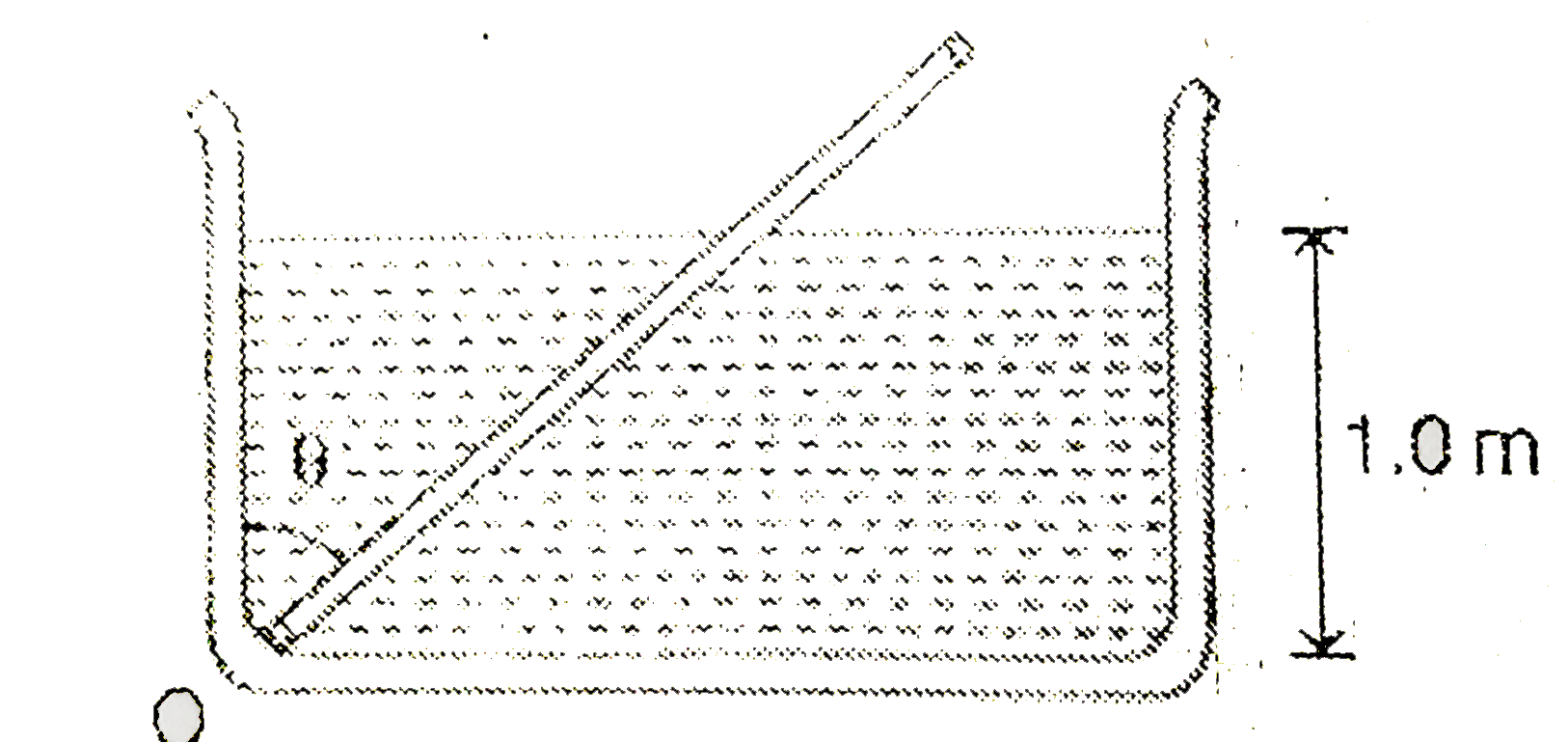
View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
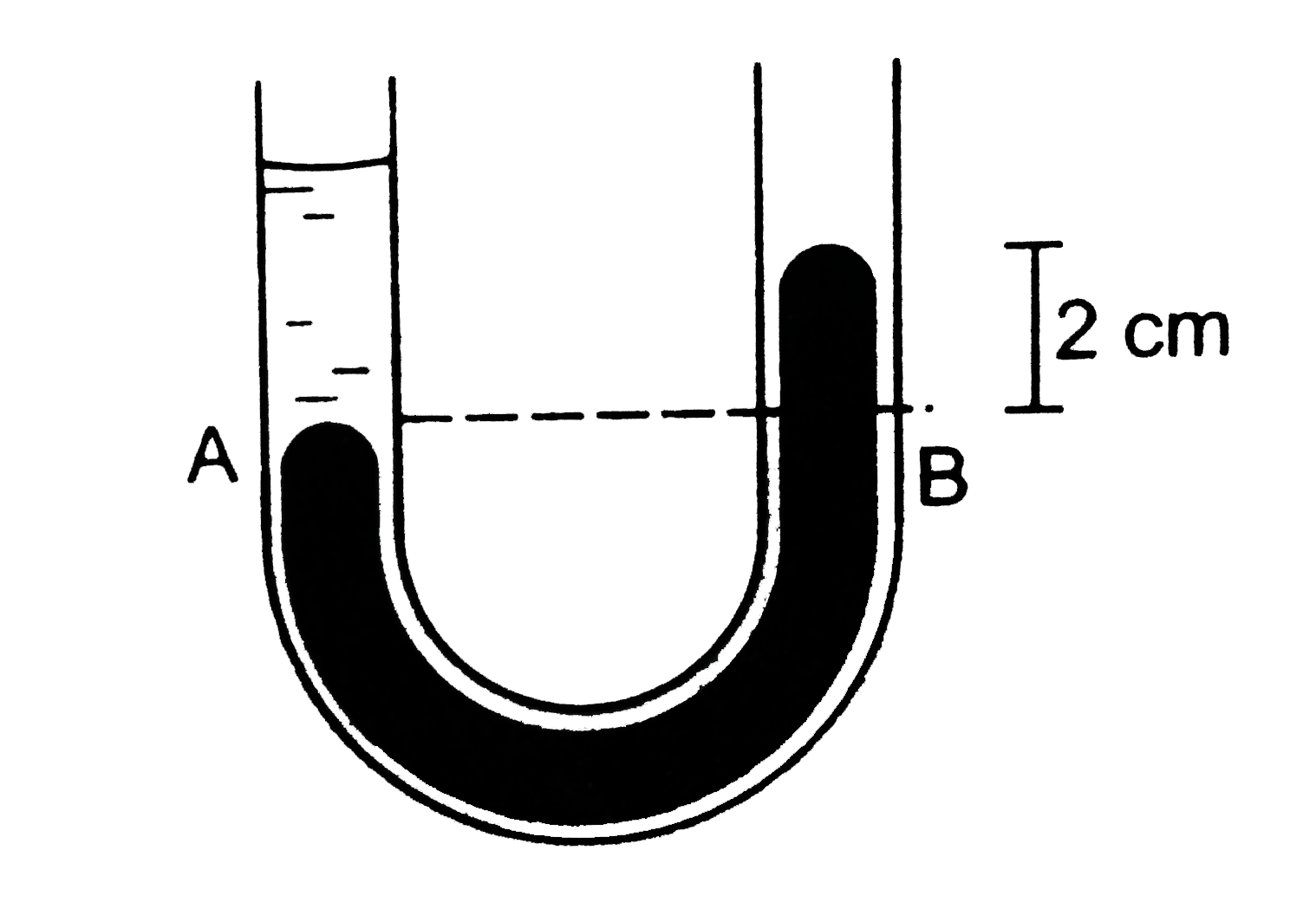 ,
,
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
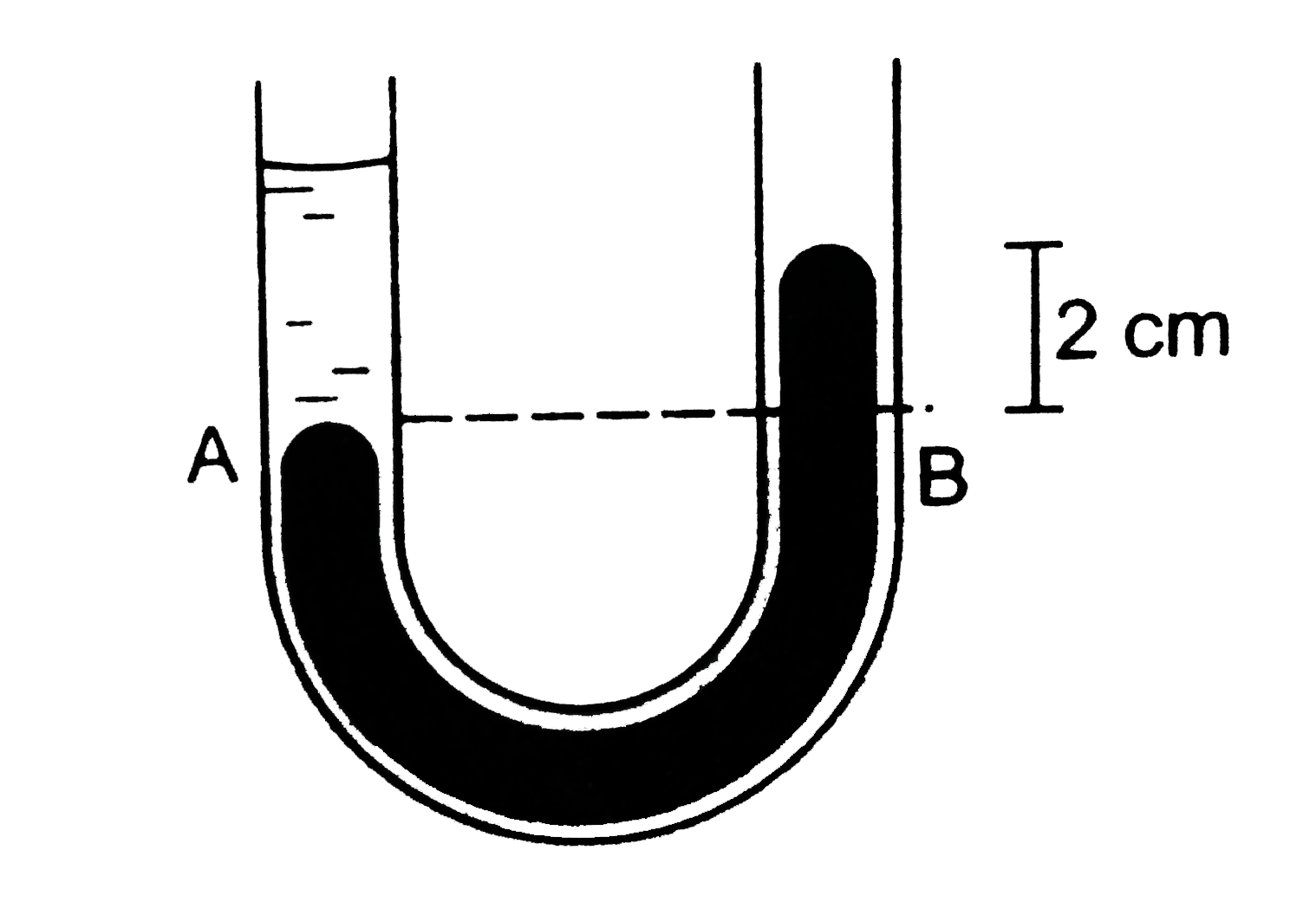 ,
,
View SolutionIf an object of mass m is taken from the surface of earth (radius R) to a height 5R, then the work done is
View SolutionA beaker containing water is kept on a spring scale. The mass of water and beaker is 5 kg . A block of mass 2 kg and specific gravity 10 is suspended by means of thread from a spring balance as shown. The readings of scales S1 and S2 are respectively Take, g=10ms−2

View Solution
