Two limbs of a manometer consist of uniform capillary tubes of radii r1andr2 respectively (r1>r2). If the level of liquid in narrower tube stands at a height .h. above that in the broader tube then the exact pressure difference will be
To solve the problem of finding the exact pressure difference between the two limbs of a manometer with capillary tubes of different radii, we can follow these steps:
Step 1: Understand the setup
We have two capillary tubes with radii r1 (broader tube) and r2 (narrower tube) where r1>r2. The liquid level in the narrower tube is at a height h above that in the broader tube.
Step 2: Define the pressures
Let p1 be the pressure in the broader tube and p2 be the pressure in the narrower tube. The height difference h indicates that the pressure in the narrower tube is lower than that in the broader tube.
Step 3: Apply the hydrostatic pressure equation
Using the hydrostatic pressure equation, we can express the relationship between the pressures and the height difference:
p1=p2+ρgh
where ρ is the density of the liquid and g is the acceleration due to gravity.
Step 4: Consider the effect of surface tension
Due to the curvature of the liquid surface in the capillary tubes, we need to account for the excess pressure caused by surface tension. The excess pressure ΔP due to surface tension S in a capillary tube is given by:
ΔP=2Sr
Thus, for the broader tube (radius r1) and the narrower tube (radius r2), we have:
p1=p1−2Sr1
p2=p2−2Sr2
Step 5: Set up the equation for pressure difference
Now, we can set up the equation for the pressure difference considering both the hydrostatic pressure and the surface tension:
p1−2Sr1=p2−2Sr2
Rearranging gives:
p1−p2=ρgh+2Sr2−2Sr1
Step 6: Final expression for pressure difference
Thus, the exact pressure difference p1−p2 can be expressed as:
p1−p2=ρgh+2S(1r2−1r1)
Conclusion
The exact pressure difference between the two limbs of the manometer is:
p1−p2=ρgh+2S(1r2−1r1)
We have two capillary tubes with radii r1 (broader tube) and r2 (narrower tube) where r1>r2. The liquid level in the narrower tube is at a height h above that in the broader tube.
Let p1 be the pressure in the broader tube and p2 be the pressure in the narrower tube. The height difference h indicates that the pressure in the narrower tube is lower than that in the broader tube.
Using the hydrostatic pressure equation, we can express the relationship between the pressures and the height difference:
p1=p2+ρgh
where ρ is the density of the liquid and g is the acceleration due to gravity.
Due to the curvature of the liquid surface in the capillary tubes, we need to account for the excess pressure caused by surface tension. The excess pressure ΔP due to surface tension S in a capillary tube is given by:
ΔP=2Sr
Thus, for the broader tube (radius r1) and the narrower tube (radius r2), we have:
p1=p1−2Sr1
p2=p2−2Sr2
Now, we can set up the equation for the pressure difference considering both the hydrostatic pressure and the surface tension:
p1−2Sr1=p2−2Sr2
Rearranging gives:
p1−p2=ρgh+2Sr2−2Sr1
Thus, the exact pressure difference p1−p2 can be expressed as:
p1−p2=ρgh+2S(1r2−1r1)
The exact pressure difference between the two limbs of the manometer is:
p1−p2=ρgh+2S(1r2−1r1)
Similar Questions
The limbs of a manometer consists of uniform capillary tubes of radii 1.44×10−3m and 7.2×104m. If the level of the liquid in the narrower tube stands 0.2 m above that in the broader tube, pressure difference between A and B is found to be 310λN/m2. Here λ is an integer. Find λ (density = 103kg/m3, surface tension = 72×10−3N/m). (take g=9.8m/s2)
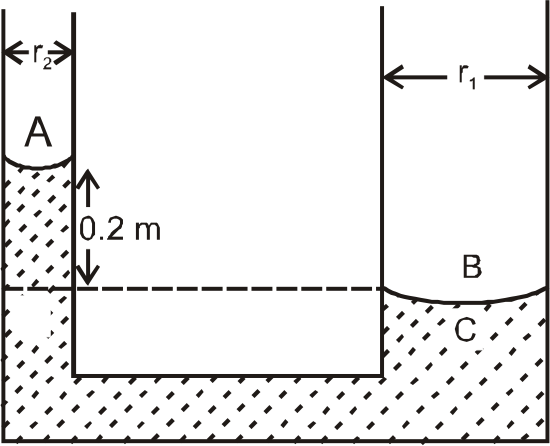
View SolutionA barometer contains two uniform capillries of radii 1.44×10−3m and 7.2×10−4m. If the height of the liquid in the narrow tube is 0.2m more than that in the wide tube, calculate the true pressure difference. Density of liquid =103kg/m3, surface tension =72×10−3N/m and g=m/s2.
View Solution
Knowledge Check
Two soap bubbles A and B have radii r1andr2 respectively. If r1<r2 than the excess pressure inside
Abubbles A and B will be equalBbubbles A will be less than that in bubbles BCbubbles A will be greater than that in bubble BDbubbles A and B will be zero.Two capillary tubes of radii 0.2 cm and 0.4 cm are dipped in the same liquid.The ratio of heights through which liquid will rise in the tube is
A1:2B2:1C1:4D4:1
A barometer contains two uniform capillaries of radii 1.4×10−3m and 7.2×10−4m. If the height of liquid in narrow tube is 0.2m more than that in wide tube, calculate the true pressure difference. Density of liquid =103kg/m3, surface tension =72×10−3N/m and g=9.8ms−12.
View SolutionTwo capillary tubes of lengths in the ratio 2:1 and radii in the ratio 1:2 are connected in series. Assume the flow of the liquid through the tube is steady. Then, the ratio of pressure difference across the tubes is
View SolutionIn a U-tube the radii of two columns are respectively r1andr2 and if a liquid of density d filled in it has level difference of h then the surface tension of the liquid is -

View SolutionA thin capillary of inner radius r1 and outer radius r2 (The inner tube is solid) is dipped in water. To how much height will the water raise in the tube ? (Assume contact angle θ→0)
View SolutionThree capillaries of length L,L2andL3 are connected in a series. Their radii are r,r2andr3 respectively. If a streamlined flow is to be maintained and pressure difference across the first capillary is ρ, then the pressure difference across the second capillary will be
View SolutionThe rate of flow of a liquid through a capillary tube of radius r is under a pressure difference of P. Calculate the rate of flow when the diameter is reduced to half and the pressure difference is made 4 P?
View Solution
