Three particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
Mass of the spherical ball at the corner .A. of the equilateral triangle = 1kg
Mass of the spherical ball at the corner .B. of the equilateral triangle = 2kg
Mass of the spherical ball at the comer .C. of the equilateral triangle = 3kg
Side of equilateral triangle = 1m
If .F. is the force of attraction between 1kg, 2kg masses then
F1=G×1×2(1)2⇒F1=2G
If .F2. is the force of attraction between 1kg, 3kg masses then
F2=G×1×3(1)2⇒F2=3G
The angle between the forces F1 and F2 is 60∘. If .FR. is the resultant of these two forces, then according to parallelogram law of vectors we can write
FR=√F21+F22+2F1F2Cosθ⇒FR=√(2G)2+(3G)2+2×2G×3G×cos60∘⇒FR=√19G
Similar Questions
Three particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
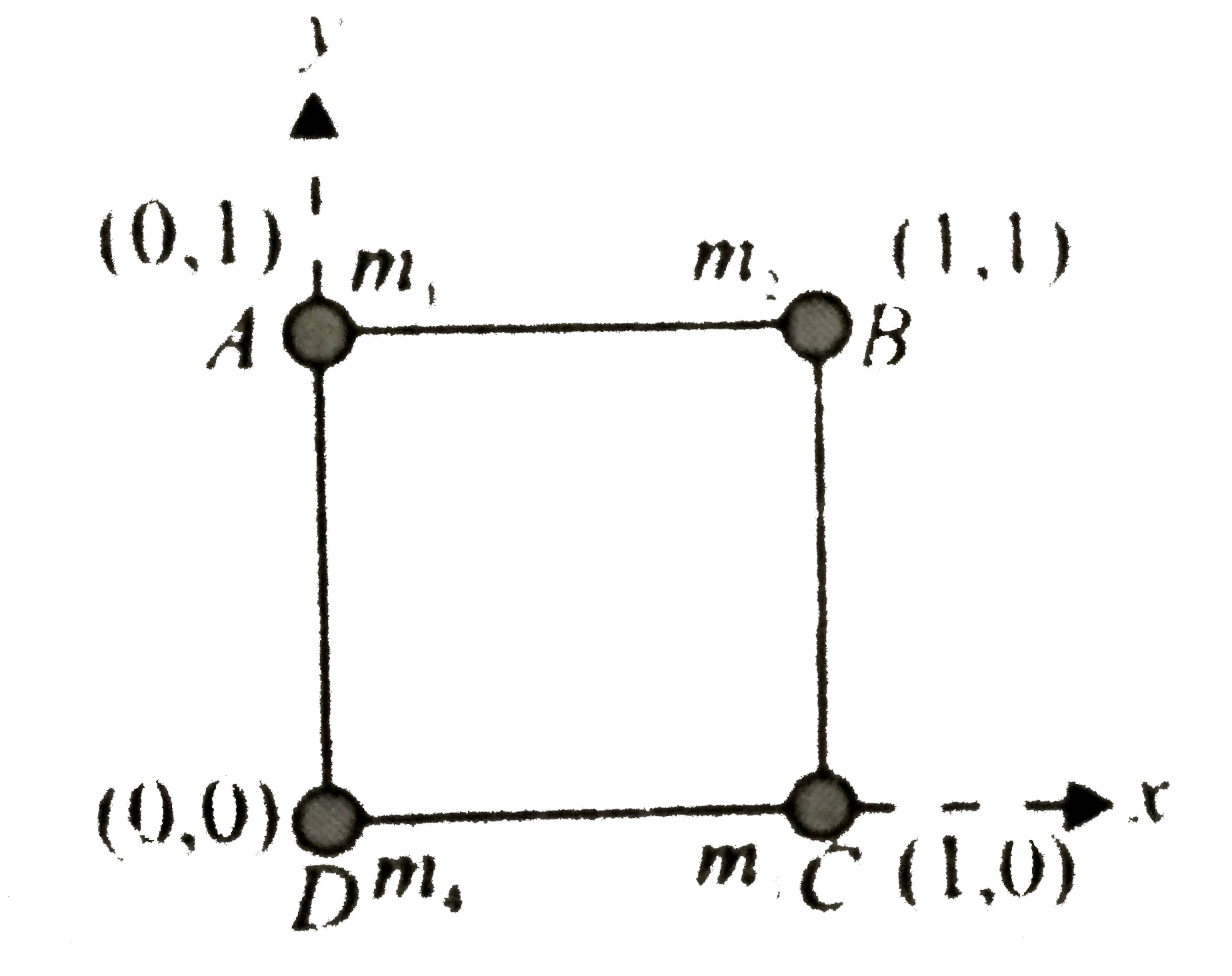
View SolutionFour particles of masses 1kg,2kg,3kg and 4kg are placed the four vertices A,B,C and D, respectively, of a square of side 1m. Find the position of centre of mass of the particles.
View Solution
Knowledge Check
Three particles of masses 1kg,32kg,and2kg are located the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
Aa. 5a9,2a3√3Bb. 2a3√3,5a9Cc. 5a9,2a√3Dd. 2a√3,5a9
4 Masses 8 kg, 2 kg, 4 kg and 2 kg are placed at the corners A, B, C, D respectively of a square ABCD of diagonal 80 cm. The distance of centre of mass from A will be
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A,B,C and D of a square of side 1m. Find square of distance of their centre of mass from A.
View SolutionThree point masses m1=2Kg,m2=4kgandm3=6kg are kept at the three corners of an equilateral triangle of side 1 m. Find the locationo of their center of mass.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles. Assume that D is situated at the origin.
View SolutionThree point particles of masses 1.0 kg 2 kg and 3 kg are placed at three comers of a right angle triangle of sides 4.0 cm , 3.0 cm and 5.0 cm as shown in the figure . The centre of mass of the system is at point :

View SolutionThree point particles of masses 1.0 kg 2 kg and 3 kg are placed at three comers of a right angle triangle of sides 4.0 cm , 3.0 cm and 5.0 cm as shown in the figure . The centre of mass of the system is at point :

View Solution