A carpet of mass M made of inextensible material is rolled along its length in the form of a cylinder of radius R and is kept on ar rough floor. The carpet starts unrolling without sliding on the floor when a negligibly small push is given to it. Calculate the horizontal velocity of the axis of the cylindrical part of the carpet when its rdius reduces to R/2.
Lose in PE due to unrolling when radius changes from R to R2 is =MgR−(MgR8)=78(MgR)
The lose in PE is equal to the gain in KE which is
K=KT+KR=12MV2+12Iω2
If .V. is the velocity when half the carpet has unrolled then as
V=Rω2,M→M4andI=12(M4)(R2)2
∴78MgR=316MV2 on solving V=(14gR3)12
Similar Questions
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.
View SolutionA floor-mat of mass M made up of extensible material, is rolled along its length so as to form a cylinder of radius R and kept on a rough horizontal surface. If the mat is now unrolled, without sliding, to a radius R2, the decrease in potential energy is
View Solution
Knowledge Check
A floor-mat of mass M made up of extensible material, is rolled along its length so as to form a cylinder of radius R and kept on a rough horizontal surface. If the mat is now unrolled, without sliding, to a radius R2, the decrease in potential energy is
A1. 12MgRB2. 78MgRC3. 58MgRD4. 34MgRA solid cylinder of mass M and radius R rolls down an inclined plane without slipping. THE speed of its centre of mass when it reaches the bottom is
A√(2gh)B√4/3.ghC√3/4.ghD√(4g/h)
A uniform solid cylinder of radius 'R' has a circular cut of radius R2 from the edge, Its mass is M. It is rolling wihtout slipping on a rough horizontal floor. When the cut part is at lowest position, centre of the disc is moving with horizontal velocity v. Choose the alternative:
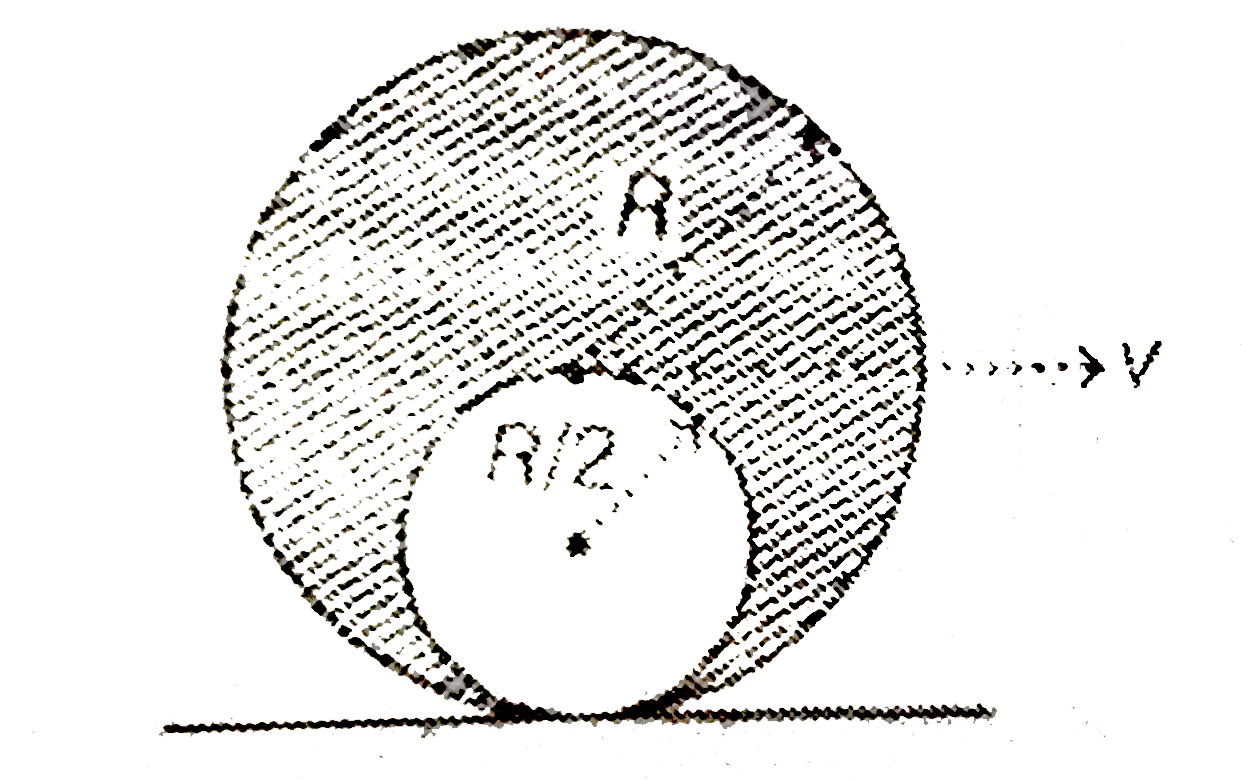
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
View SolutionA cylinder of mass m and radius R is kept on a rough surface after giving its centre a horizontal speed v0. Find the speed of the centre of the cylinder when it stops slipping.
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionA uniform rope of length l and mass m lies on a smooth horizontal table with its length perpendicular to the edge of the table and a small part of the rope having over the edge. The rope starts sliding from rest under the weight of the over hanging end. The velocity of the rope when the length of the hanging part is . x
View SolutionA uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. After t0 seconds, it acquires pure rolling motion as shown in the figure.
(a) Calculate the velocity of the center of mass of the disc at t0.
Assuming that the coefficent of friction to be μ, calculate t0.

View Solution