The gravitational potential at centre of earth is
−2GMR
−3GM2R
3GM2R
−GM2R
The correct Answer is:B
To find the gravitational potential at the center of the Earth, we can follow these steps:
1. Understanding Gravitational Potential:
The gravitational potential V at a distance r from a mass M is given by the formula:
V=−GMr
where G is the gravitational constant.
2. Consider a Thin Spherical Shell:
Imagine a thin spherical shell of thickness dx at a distance x from the center of the Earth. The mass dm of this shell can be expressed in terms of its density ρ and volume.
3. Mass of the Shell:
The volume dV of the thin shell is given by:
dV=4πx2dx
Therefore, the mass dm of the shell is:
dm=ρ⋅dV=ρ⋅4πx2dx
4. Gravitational Potential Contribution from the Shell:
The potential dV due to this thin shell at the center of the Earth is:
dV=−Gdmx=−Gρ⋅4πx2dxx
Simplifying this gives:
dV=−Gρ⋅4πxdx
5. Integrate to Find Total Potential:
To find the total gravitational potential V at the center of the Earth, integrate dV from x=0 to x=R (where R is the radius of the Earth):
V=∫R0−Gρ⋅4πxdx
This integrates to:
V=−Gρ⋅4π(x22)R0=−Gρ⋅4π⋅R22
6. Expressing in Terms of Mass:
The mass M of the Earth can be expressed as:
M=ρ⋅43πR3
Substituting ρ in the potential equation gives:
V=−32GMR
7. Final Result:
At the center of the Earth, the gravitational potential is:
V=−32GMR
Conclusion:
Thus, the gravitational potential at the center of the Earth is −32GMR.
---
The gravitational potential V at a distance r from a mass M is given by the formula:
V=−GMr
where G is the gravitational constant.
Imagine a thin spherical shell of thickness dx at a distance x from the center of the Earth. The mass dm of this shell can be expressed in terms of its density ρ and volume.
The volume dV of the thin shell is given by:
dV=4πx2dx
Therefore, the mass dm of the shell is:
dm=ρ⋅dV=ρ⋅4πx2dx
The potential dV due to this thin shell at the center of the Earth is:
dV=−Gdmx=−Gρ⋅4πx2dxx
Simplifying this gives:
dV=−Gρ⋅4πxdx
To find the total gravitational potential V at the center of the Earth, integrate dV from x=0 to x=R (where R is the radius of the Earth):
V=∫R0−Gρ⋅4πxdx
This integrates to:
V=−Gρ⋅4π(x22)R0=−Gρ⋅4π⋅R22
The mass M of the Earth can be expressed as:
M=ρ⋅43πR3
Substituting ρ in the potential equation gives:
V=−32GMR
At the center of the Earth, the gravitational potential is:
V=−32GMR
Thus, the gravitational potential at the center of the Earth is −32GMR.
Similar Questions
A diametrical tunnel is dug across the earth. A ball dropped into the tunnel from one side. The velocity of the ball when it reaches the centre of the earth is [Given: gravitational potential at the centre of earth =−3/2(GM/R)]
View SolutionThe gravitational potential at the centre of a square of side a when four point masses m each are kept at its vertices will be
View Solution
Knowledge Check
Two spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
A−GMrB−2GMrC−GM2rD−4GMr
A thin of length L is bent to form a semicircle. The mass of rod is M. What will be the gravitational potential at the centre of the circle ?
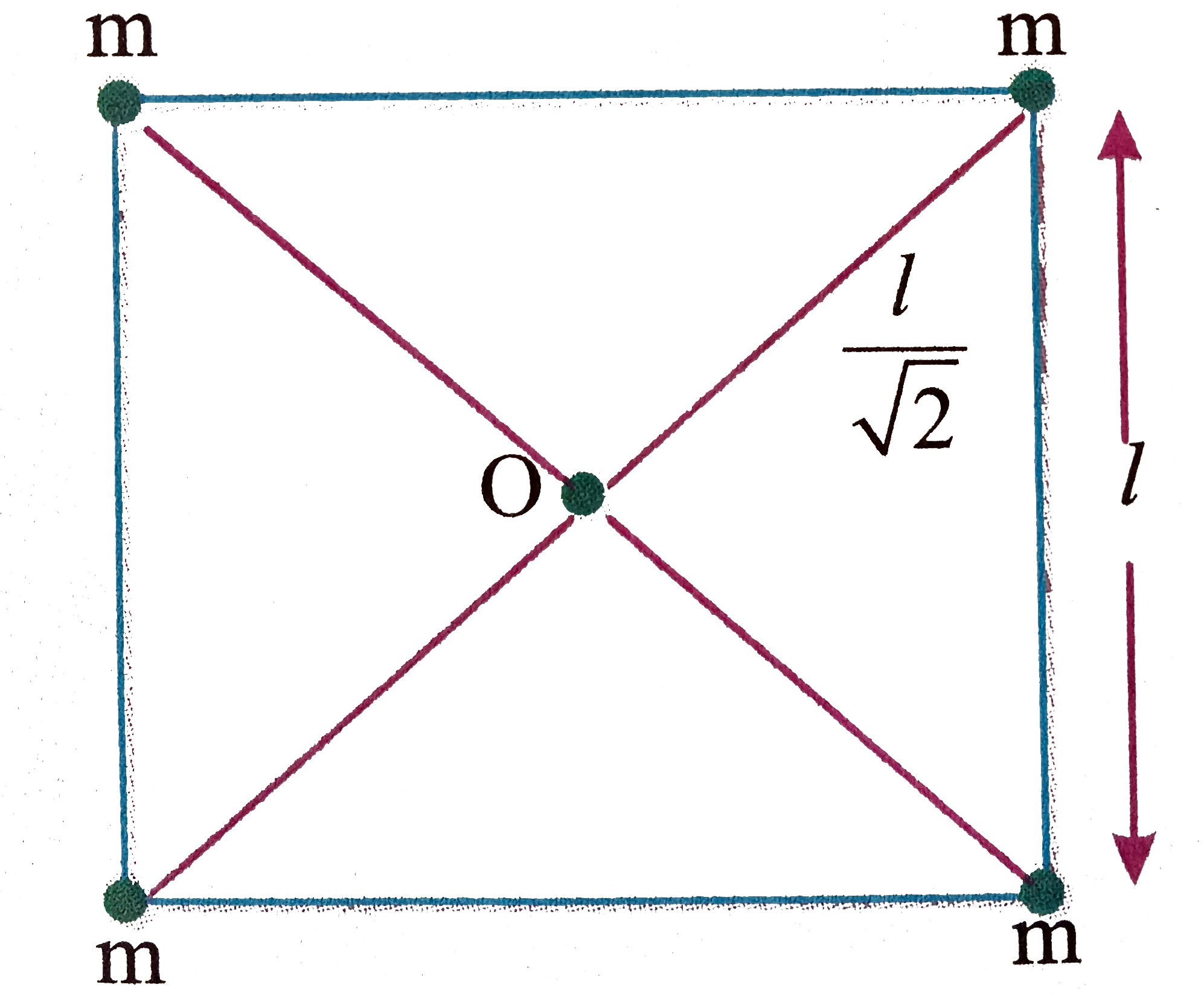
View SolutionFind the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
View SolutionA hollow spherical shell is compressed to half its radius. The gravitational potential at the centre
View SolutionA uniform spherical shell gradually shrinks maintainig its shape. The gravitational potential at the centre
View SolutionWhat is the gravitational potential energy of the earth and a satellite of mass m=100kg orbiting close to the earth's surface ?
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View Solution
