If the area swept by the line joining the sun and the earth from Feb 1 to Feb 7 is .A., then the area swept by the radius vector from Feb 8 to Feb 28 is
A
2A
3A
4A
The correct Answer is:C
To solve the problem, we will use Kepler's second law, which states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
1. Identify the Given Information:
- Area swept from February 1 to February 7 is A.
- The time interval from February 1 to February 7 is 7 days.
2. Calculate the Area Swept per Day:
- Since the area swept in 7 days is A, the area swept in 1 day can be calculated as:
Area per day=A7
3. Determine the Time Interval from February 8 to February 28:
- The number of days from February 8 to February 28 is 21 days.
4. Calculate the Total Area Swept from February 8 to February 28:
- The total area swept in 21 days can be calculated by multiplying the area swept per day by the number of days:
Area for 21 days=21×(A7)
- Simplifying this gives:
Area for 21 days=21A7=3A
5. Final Answer:
- Therefore, the area swept by the radius vector from February 8 to February 28 is 3A.
- Area swept from February 1 to February 7 is A.
- The time interval from February 1 to February 7 is 7 days.
- Since the area swept in 7 days is A, the area swept in 1 day can be calculated as:
Area per day=A7
- The number of days from February 8 to February 28 is 21 days.
- The total area swept in 21 days can be calculated by multiplying the area swept per day by the number of days:
Area for 21 days=21×(A7)
- Simplifying this gives:
Area for 21 days=21A7=3A
- Therefore, the area swept by the radius vector from February 8 to February 28 is 3A.
Similar Questions
A rocket is launched normal to the surface of the earth, away from the sun, along the line joining the sun and the earth. The sun is 3×105 times heavier than the earth and is at a distance 2.5×104 times larger than the radius of the earth. the escape velocity from earth's gravitational field is ue=11.2kms−1. The minmum initial velocity (ue)=11.2kms−1. the minimum initial velocity (us) required for the rocket to be able to leave the sun-earth system is closest to (Ignore the rotation of the earth and the presence of any other planet
View SolutionFigure shows the elipticla path of a planet about the sun. The two shaded parts have equal area. If t1andt2 be the tim taken by the planet to go from a to b and from c to d respectively
View Solution
Knowledge Check
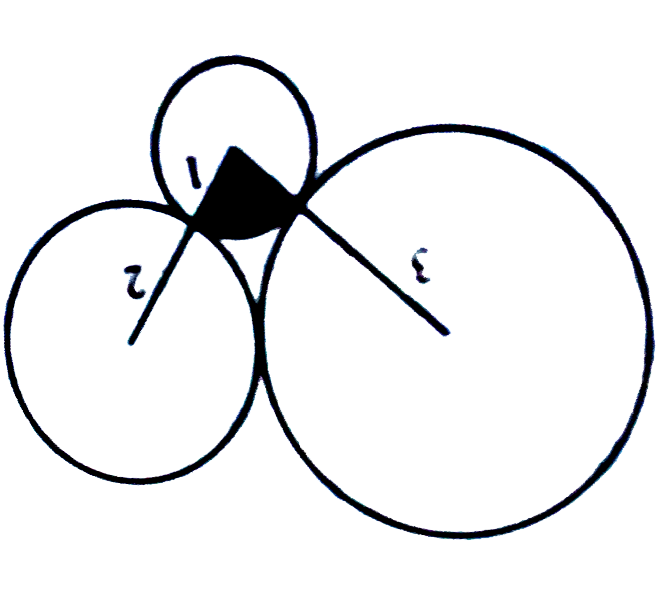
Three circles with radii 1,2 and 3 inches are externally tangent to one another , as shown in the figure above . The area , in square inches , of the sector of the circle of radius 1 that is cut off by the line segments joining the center of that circle to the centers of the other two circles (the shaded area ) isAπBπ2Cπ3Dπ4
A particle of mass m is travelling with a constant velocity v=v0ˆi along the line y=b,z=0. Let dA be the area swept out by the position vector from origin to the particle in time dt and L the magnitude of angular momentum of particle about origin at any time t. Then
View SolutionThe solar constant is the amount of heat energy received per second per unit area of a perfectly black surface placed at a mean distance of the Earth form the Sun, in the absence of Earth's atmosphere, the surface being held perpendicular to the direction of Sun's rays. Its value is 1388W/m2. If the solar constant for the earth is 's'. The surface temperature of the sun is TK,D is the diameter of the sun, R is the mean distance of the Earth from the sun. The sun subtends a small angle 'theta' at the earth. Then correct options is/are:-
View SolutionIn Rutherford's nuclear model of the atom, the nucleus (radius about 10−15m) is analogous to the sun about which the electron moves in orbit (radius about 10−10m) like the earth orbits around the sun. If the dimensions of the solar system had the same proportions as those of the atom, would the earth be closer to or further away form the sun than actually it is ? The radius of earth's orbit is about is 1.5×1011m. The radius of the sun is taken as 7×108m.
View SolutionCompare the distance of the sun from the earth and the distance of the mars from the Earth if the Sun is 1.5×108 km from the Earth and the Mars is 5.5×107 km from the Earth.
View SolutionA circular area of radius 1.0 cm is placed at a distance of 2.0 m from a poit source.Teh source emits light uniformluy in al directions. The line joining the sorce to the dcentre of the area is normal to the area. It ils found that 2.0×1−3 lumen of luminous flux is incident on the area. Calculate the total luminous flux emitted by the soure and teh luminous intensity of the source along the axis of the area.
View SolutionA plane P = 0 is the perependicular bisector of the line joining the points (2, 3, 4) and (6, 7, 8). The perpendicular distance of P = 0 from the origin is
View SolutionIf d is the distance between the centre of the earth of mass M1 and the moon of mass M2, then the velocity with which a body should be projected from the mid point of the line joining the earth and the moon, so that it just escape is
View Solution