A vertical force Facts on the cross-seaction of a cylinder body of radius .r. and length L. If Y is young.s modulus and σ = possoing ratio, find the change in volume of the body?
The correct Answer is:FL(1−2σ)Y
To find the change in volume of a cylindrical body subjected to a vertical force, we can follow these steps:
Step 1: Understand the Geometry of the Cylinder
The volume V of a cylinder is given by the formula:
V=πr2L
where r is the radius and L is the length of the cylinder.
Step 2: Relate Change in Volume to Strain
The change in volume ΔV can be expressed in terms of the original volume V and the strains in the radial and longitudinal directions:
ΔVV=2Δrr+ΔLL
where Δr is the change in radius and ΔL is the change in length.
Step 3: Use Poisson's Ratio
Poisson's ratio σ relates the change in radius to the change in length:
σ=−Δr/rΔL/L
From this, we can express Δrr in terms of ΔL:
Δrr=−σΔLL
Step 4: Substitute into the Volume Change Equation
Substituting Δrr into the volume change equation gives:
ΔVV=2(−σΔLL)+ΔLL
This simplifies to:
ΔVV=−2σΔLL+ΔLL
ΔVV=(1−2σ)ΔLL
Step 5: Relate Change in Length to Stress
The change in length ΔL can be related to the applied force F using the formula for stress and Young's modulus Y:
Stress=FA=Fπr2
Strain=ΔLL=StressY=FYπr2
Thus,
ΔLL=FYπr2
Step 6: Substitute Back to Find Change in Volume
Now substituting ΔLL back into the volume change equation:
ΔVV=(1−2σ)(FYπr2)
Thus, the change in volume ΔV can be expressed as:
ΔV=V⋅ΔVV=πr2L⋅(1−2σ)(FYπr2)
This simplifies to:
ΔV=L⋅(1−2σ)(FY)
Final Answer
The change in volume of the body is:
ΔV=L(1−2σ)FY
The volume V of a cylinder is given by the formula:
V=πr2L
where r is the radius and L is the length of the cylinder.
The change in volume ΔV can be expressed in terms of the original volume V and the strains in the radial and longitudinal directions:
ΔVV=2Δrr+ΔLL
where Δr is the change in radius and ΔL is the change in length.
Poisson's ratio σ relates the change in radius to the change in length:
σ=−Δr/rΔL/L
From this, we can express Δrr in terms of ΔL:
Δrr=−σΔLL
Substituting Δrr into the volume change equation gives:
ΔVV=2(−σΔLL)+ΔLL
This simplifies to:
ΔVV=−2σΔLL+ΔLL
ΔVV=(1−2σ)ΔLL
The change in length ΔL can be related to the applied force F using the formula for stress and Young's modulus Y:
Stress=FA=Fπr2
Strain=ΔLL=StressY=FYπr2
Thus,
ΔLL=FYπr2
Now substituting ΔLL back into the volume change equation:
ΔVV=(1−2σ)(FYπr2)
Thus, the change in volume ΔV can be expressed as:
ΔV=V⋅ΔVV=πr2L⋅(1−2σ)(FYπr2)
This simplifies to:
ΔV=L⋅(1−2σ)(FY)
The change in volume of the body is:
ΔV=L(1−2σ)FY
Similar Questions
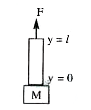
A vertical force of magnitude Facts at the top of a string of mass 'm' and length 'l'. A body of mass M hangs at the bottom of the string.
View SolutionTwo wire A and B of length l, radius r and length 2l, radius 2r having same Young's modulus Y are hung with a width mg, fig. What is the net elongation in the two wires?
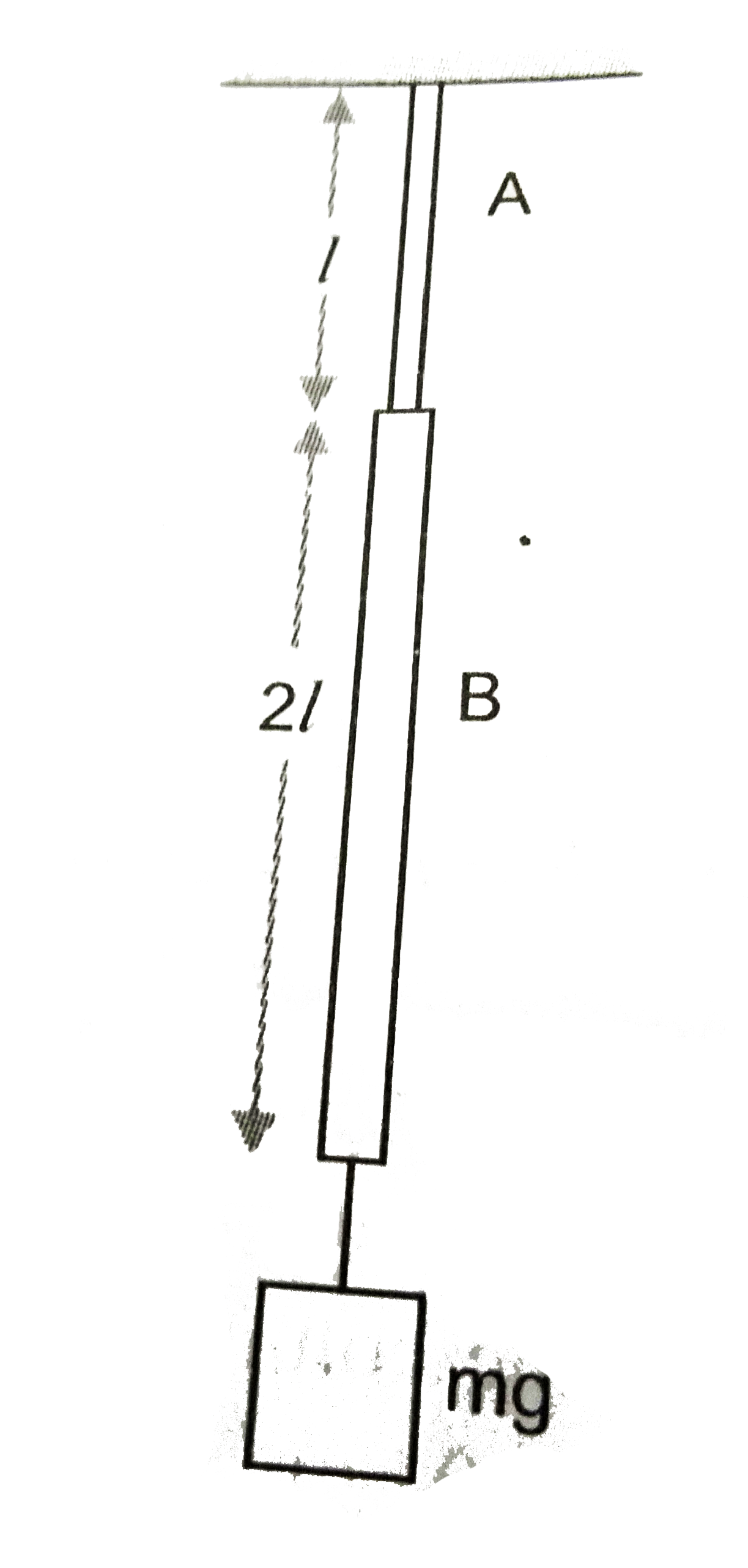
View Solution
Knowledge Check
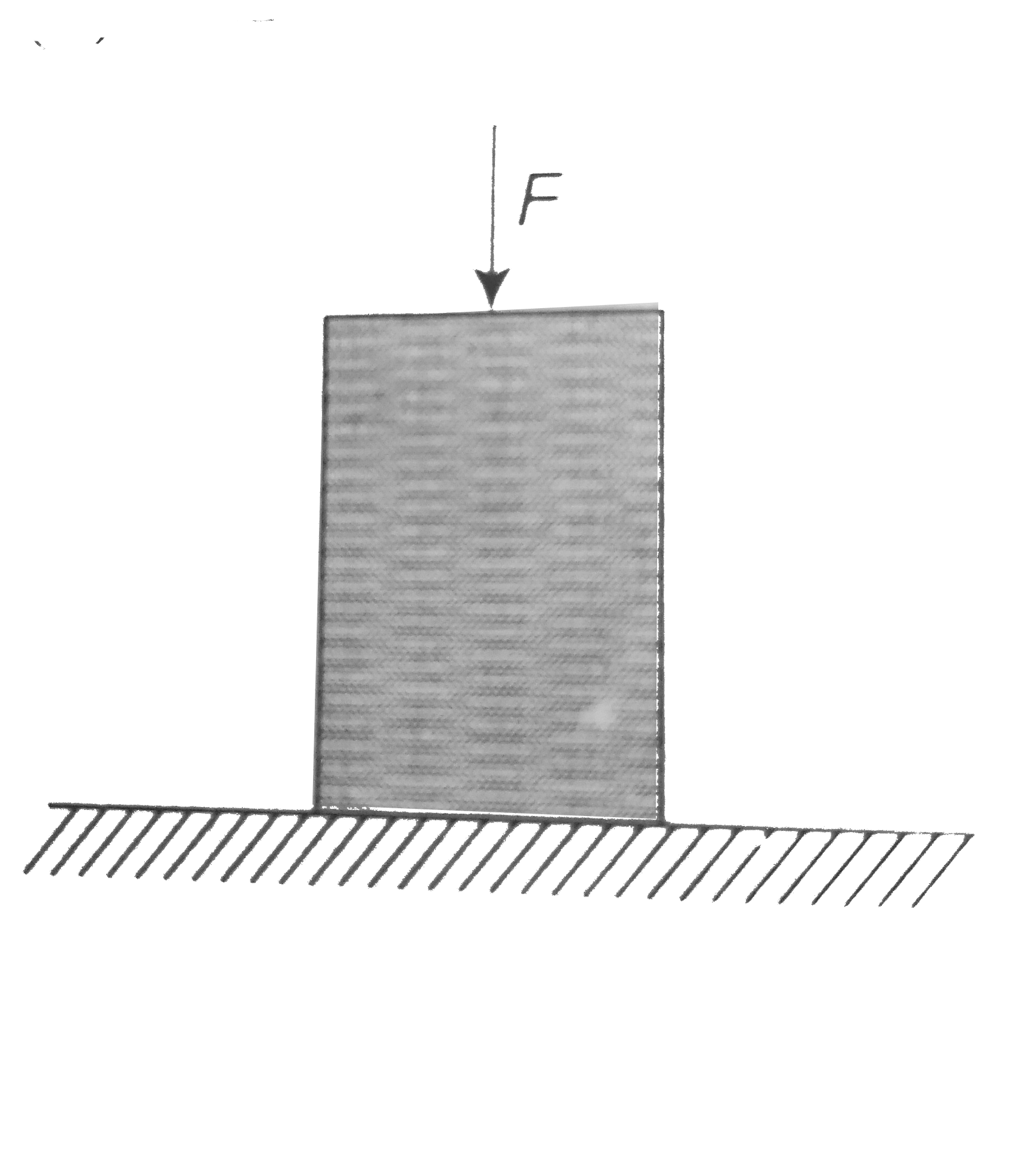
A metal cylinder of length L is subjected to a uniform compressive to a uniform compressive force F as shown in the figure. The material of the cylinder has Young's modulus Y and poisson's ratio σ The change in volume of the cylinder isAsigamFLYB(1−σ)FLYC(1+2σ)FLYD(1−2σ)FLYA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAl
A vertical metal cylinder of radius 2 cm and length 2 m is fixed at the lower end and a load of 100 kg is put on it. find a. the stress b. the strain and c. the compression of the cylinder. Young modulus of the metal =2×1011Nm−2
View SolutionA uniform ring of radius R and made up of a wire of cross - sectional radius r is rotated about its axis with a frequency f. If density of the wire is ρ and young's modulus is Y . Find the fractional change in radius of the ring .
View SolutionA wire of natural length l, young's modulus Y and area of cross-section A is extended by x. Then, the energy stored in the wire is given by
View SolutionA force F is applied onn a spool (mass m and radius R) in vertical direction as shown in case I and case II. The radius of gyration k of spool is R/(√2). Assuming pure rolling, find the acceleration of the CM of the body, assuming it as a uniform cylinder of mass m.

View SolutionA wooden wheel of radius R is made of two semicircular part . The two parts are held together by a ring made of a metal strip of cross sectional area S and length L. L is slightly less than 2πR. To fit the ring on the wheel, it is heated so that its temperature rises by ΔTand it just steps over the wheel. As it cools down to surrounding temperature, it process the semicircle parts together. If the coefficient of linear expansion of the metal is α, and it Young's modulus is Y, the force that one part of the wheel applies on the other part is :

View SolutionA uniform rod of mass m is hinged at one end and other end is connected to a light extensible string having length L.If the Youngs modulus and crosssectional area of the wire is Y and A respectively then the elongation in the string is
View Solution
