A brass wire 300 cm long when subjected to a force F produces an elongation .a.. Another wire of twice the diameter and of same length and material, when subjected to the same force F, produces an elongation .b.. What is the value of a/b ?
The correct Answer is:4
To solve the problem, we need to use the relationship between stress, strain, and the properties of the materials involved. The elongation of a wire under a tensile force can be described by the formula:
ΔL=F⋅LA⋅Y
where:
- ΔL is the elongation,
- F is the applied force,
- L is the original length of the wire,
- A is the cross-sectional area,
- Y is Young's modulus of the material.
Step 1: Identify the parameters for both wires
- For the first wire:
- Length L1=300cm
- Elongation ΔL1=a
- Diameter d1
- Radius r1=d12
- Area A1=πr21
- For the second wire:
- Length L2=300cm (same length)
- Elongation ΔL2=b
- Diameter d2=2d1 (twice the diameter)
- Radius r2=d22=d1
- Area A2=πr22=π(2r1)2=4πr21
Step 2: Write the elongation formulas
Using the elongation formula for both wires:
1. For the first wire:
a=F⋅L1A1⋅Y=F⋅300πr21⋅Y
2. For the second wire:
b=F⋅L2A2⋅Y=F⋅3004πr21⋅Y
Step 3: Find the ratio a/b
Now, we can find the ratio of the elongations a and b:
ab=F⋅300πr21⋅YF⋅3004πr21⋅Y=4πr21⋅Yπr21⋅Y
This simplifies to:
ab=4
Final Answer
Thus, the value of ab=4.
---
- ΔL is the elongation,
- F is the applied force,
- L is the original length of the wire,
- A is the cross-sectional area,
- Y is Young's modulus of the material.
- For the first wire:
- Length L1=300cm
- Elongation ΔL1=a
- Diameter d1
- Radius r1=d12
- Area A1=πr21
- Length L2=300cm (same length)
- Elongation ΔL2=b
- Diameter d2=2d1 (twice the diameter)
- Radius r2=d22=d1
- Area A2=πr22=π(2r1)2=4πr21
Using the elongation formula for both wires:
a=F⋅L1A1⋅Y=F⋅300πr21⋅Y
b=F⋅L2A2⋅Y=F⋅3004πr21⋅Y
Now, we can find the ratio of the elongations a and b:
Thus, the value of ab=4.
Similar Questions
Two wires of the same material and length are stretched by the same force. Their masses are in the ratio 3:2. Their elongations are in the ratio
View SolutionTwo wires of the same material and same mass are stretched by the same force. Their lengths are in the ratio 2:3. Their elongation are in the ratio
View Solution
Knowledge Check
A wire is stretched by 10 mm when it is pulled bya certain force. Another wire of the same material but double the length and double the diameter is stretched by the same force. The elongation of the second wire is
A5 mmB10 mmC20 mmD40 mm
_E01_007_Q01.png)
The load versus elongation graph for four wires of the same material and same length is shown in the figure. The hinnest wire is represented by the line
View SolutionTwo wires of the same length and same material but radii in the ratio of 1:2 are stretched by unequal forces to produce equal elongation. The ratio of the two forces is
View SolutionIf in case A, elongation in wire of length L is l then for same wire elongation in case B will be
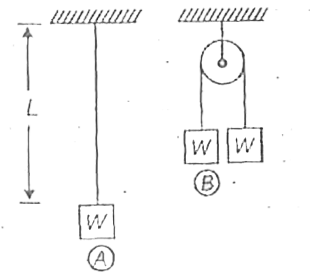
View SolutionA wire of length is stretched by a force F to cause an extension x. Another wire of same material and same volume but 50% larger in length than the first wire, the force required for the same extension will be
View SolutionA wire is stretched 1mm by a force of 1kN. How far would a wire of the same material and length but of four times that diameter be stretched by the same force?
View SolutionIn an experiment, brass and steel wires of length 1 m each with areas of cross section 1mm2 are used. The wires are connected in series and one end of the combined wire is connected to a rigid support and other end is subjected to elongation. The stress required to produce a net elongation of 0.2 mm is, [Given, the Young’s Modulus for steel and brass are, respectively, 120×109N/m2and60×109N/m2
View SolutionIn an experiment, brass and steel wires of length 1 m each with areas of cross section 1mm2 are used. The wires are connected in series and one end of the combined wire is connected to a rigid support and other end is subjected to elongation. The stress required to produce a net elongation of 0.2 mm is, [Given, the Young’s Modulus for steel and brass are, respectively, 120×109N/m2and60×109N/m2
View Solution
