A real gas can be approximated to an idcal gas at
low density
high pressure
high density
low temperature
The correct Answer is:A
To determine the conditions under which a real gas can be approximated as an ideal gas, we can analyze the behavior of gases under different conditions. Here’s a step-by-step solution:
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = universal gas constant
- T = temperature
Step 2: Identify Conditions for Ideal Behavior
Real gases deviate from ideal behavior under certain conditions. Generally, a real gas behaves more like an ideal gas when:
1. The pressure is low.
2. The temperature is high.
3. The density is low.
Step 3: Analyze the Given Options
The options provided are:
- Low density
- High pressure
- High density
- Low temperature
Step 4: Evaluate Each Option
- Low Density: This condition allows gas molecules to be far apart, minimizing intermolecular forces, which makes the gas behave more ideally. (Correct)
- High Pressure: At high pressure, gas molecules are closer together, leading to significant intermolecular forces, causing deviations from ideal behavior. (Incorrect)
- High Density: Similar to high pressure, high density implies that molecules are close together, which leads to non-ideal behavior. (Incorrect)
- Low Temperature: At low temperatures, gas molecules have lower kinetic energy, which increases the effect of intermolecular forces, leading to deviations from ideal behavior. (Incorrect)
Step 5: Conclusion
From the analysis, the only condition under which a real gas can be approximated to an ideal gas is at low density.
Final Answer
A real gas can be approximated to an ideal gas at low density.
---
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = universal gas constant
- T = temperature
Real gases deviate from ideal behavior under certain conditions. Generally, a real gas behaves more like an ideal gas when:
1. The pressure is low.
2. The temperature is high.
3. The density is low.
The options provided are:
- Low density
- High pressure
- High density
- Low temperature
- Low Density: This condition allows gas molecules to be far apart, minimizing intermolecular forces, which makes the gas behave more ideally. (Correct)
- High Pressure: At high pressure, gas molecules are closer together, leading to significant intermolecular forces, causing deviations from ideal behavior. (Incorrect)
- High Density: Similar to high pressure, high density implies that molecules are close together, which leads to non-ideal behavior. (Incorrect)
- Low Temperature: At low temperatures, gas molecules have lower kinetic energy, which increases the effect of intermolecular forces, leading to deviations from ideal behavior. (Incorrect)
From the analysis, the only condition under which a real gas can be approximated to an ideal gas is at low density.
A real gas can be approximated to an ideal gas at low density.
Similar Questions
Knowledge Check
The molecules of a gas are in constant (i) _______ motion . They move in (ii) ________ lines until they collide with another molecule . The collisions are perfectly (iii) _________ in nature . A real gas behaves as an ideal gas at (iv) _________ temperature and (v) _________ pressure .
A (i) (ii) (iii)(iv)(v)randomverticalstraighthighlowB (i) (ii) (iii)(iv)(v)straightrandomelasticlowhighC (i) (ii) (iii)(iv)(v)randomstraightelastichighlowD (i) (ii) (iii)(iv)(v)idealroundelasticlowhigh
Boyle's temperature or Boyle point is the temperature at which a real gas starts behaving like an ideal gas over a particular range of pressure. A graph is plotted between compressibility factor Z and pressure P.

What is the deviation of real gas from ideal behaviour in terms of compressibility factor , Z ?
View SolutionAssertion : The pressure of real gas is less than the pressure of ideal gas. Reason : Intermolecular forces of attraction in real gases are greater than in ideal gas.
View SolutionAssertion : The pressure of real gas is less than the pressure of ideal gas. Reason : Intermolecular forces of attraction in real gases are greater than in ideal gas.
View SolutionAt point P and Q, the real gas deviation with respect to ideal gas is respectively :
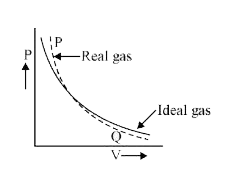
View SolutionPressure versus volume graph for real gas and are shown in figure. Answer the following question on the basis of this graph.
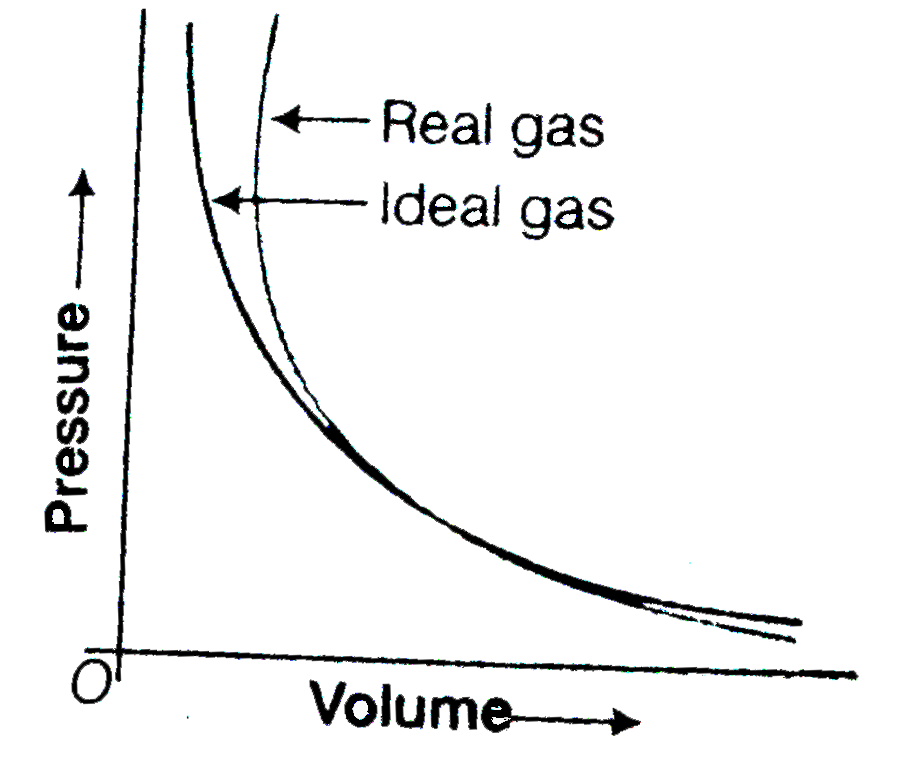
(i) Interpret the behaviour of real gas with respect to ideal gas at low pressure.
(ii) Interpret the behaviour of real gas with respect to ideal gas at high pressure.
(iii) Mark the pressure and volume by drawing a line at the point where real gas behaves as an ideal gas.
View SolutionWhat is an ideal (or perfect) gas ? Under what condition of pressure and temperature can a gas be assumed as an ideal gas ? Determine the gas constant for one gram molecule of a gas.
View SolutionStatement-1 : At low pressure and high temperature real gas approaches the ideal gas behaviour.
and
Statement-2 : At low prossure and high temperature the molecules are negligible.
View Solution
