Density of liquid at any temperature 't' is given by . This equation applies to
all liquids
all liquids except water
no liquid
all liquids except mercury
The correct Answer is:B
To solve the question regarding the density of a liquid at any temperature 't', given by the equation:
dt=d01+gt
we need to analyze the context of this equation and its applicability to different types of liquids.
1. Understanding the Equation:
- The equation states that the density dt of a liquid at temperature t is equal to the initial density d0 divided by 1+gt, where g is a constant that represents the coefficient of volume expansion of the liquid.
2. Analyzing the Variables:
- d0: Density of the liquid at a reference temperature (usually at 0 degrees Celsius).
- g: Coefficient of volume expansion, which is a property of the liquid that indicates how much the volume changes with temperature.
- t: The temperature at which we want to find the density.
3. Identifying the Applicability:
- This equation is generally applicable to most liquids, as they tend to expand uniformly with temperature, leading to a decrease in density as temperature increases.
- However, water exhibits an anomalous behavior, particularly between 0 degrees Celsius and 4 degrees Celsius, where it actually contracts instead of expanding. This means that the relationship described by the equation does not hold true for water in that temperature range.
4. Conclusion:
- Since the equation does not apply to water due to its unique properties, we can conclude that the equation is valid for all liquids except water.
Final Answer:
The equation applies to all liquids except water.
- The equation states that the density dt of a liquid at temperature t is equal to the initial density d0 divided by 1+gt, where g is a constant that represents the coefficient of volume expansion of the liquid.
- d0: Density of the liquid at a reference temperature (usually at 0 degrees Celsius).
- g: Coefficient of volume expansion, which is a property of the liquid that indicates how much the volume changes with temperature.
- t: The temperature at which we want to find the density.
- This equation is generally applicable to most liquids, as they tend to expand uniformly with temperature, leading to a decrease in density as temperature increases.
- However, water exhibits an anomalous behavior, particularly between 0 degrees Celsius and 4 degrees Celsius, where it actually contracts instead of expanding. This means that the relationship described by the equation does not hold true for water in that temperature range.
- Since the equation does not apply to water due to its unique properties, we can conclude that the equation is valid for all liquids except water.
The equation applies to all liquids except water.
Similar Questions
For a certain reaction the variation of rate constant with temperature is given by the equation
lnkt=lnk0+(ln3)t10(t≥0∘C)
The value of temperature coefficient of the reaction is
View SolutionFor a certain reaction the variation of rate constant with temperature is given by the equation
lnkt=lnk0+(ln3)t10(t≥0∘C)
The value of temperature coefficient of the reaction is
View SolutionA wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given by
View SolutionSolids and liquids both expands on heating. The density of substance decreases on expanding according to the relation ρ2=ρ11+γ(T2−T1), where , ρ1→density atT1,ρ2→density atT2,γ→ coefficient of volume expansion of substances. When a solid is submerged in a liquid , liquid exerts an upward force on solid which is equal to the weight of liquid displaced by submerged part of solid. Solid will float or sink depends on relative densities of solid and liquid . A cubical block of solid floats in a liquid with half ot its volume submerged in liquid as shown in figure (at temperature T) αS→ Coefficient of linear expansion of solid
γL→Coefficient of volume expansion of liquid
ρS→Density of solid at temperatureT
ρL→ Density of liquid at temperatureT
_E01_197_Q01.png)
The relation between densities of solid and liquid at temperature T is
View SolutionThe displacement of a body is given by s=12gt2 where g is acceleration due to gravity. The velocity of the body at any time t is
View SolutionDensity of gas is inversely proportional to absolute temperature and directly proportional to pressure
⇒d∝PT⇒dTP = constant ⇒d1T1P1=d2T2P2
Density at a particular temperature and pressure can be calculated bousing ideal gas equation
PV=nRT⇒PV=massmolar mass (M)xRT
P×M=massvolume×RT⇒P×M=d×RT
d=PMRT
The density of gas is 3.8 g L−1 at STP. The density at 27°C and 700 mm Hg pressure will be
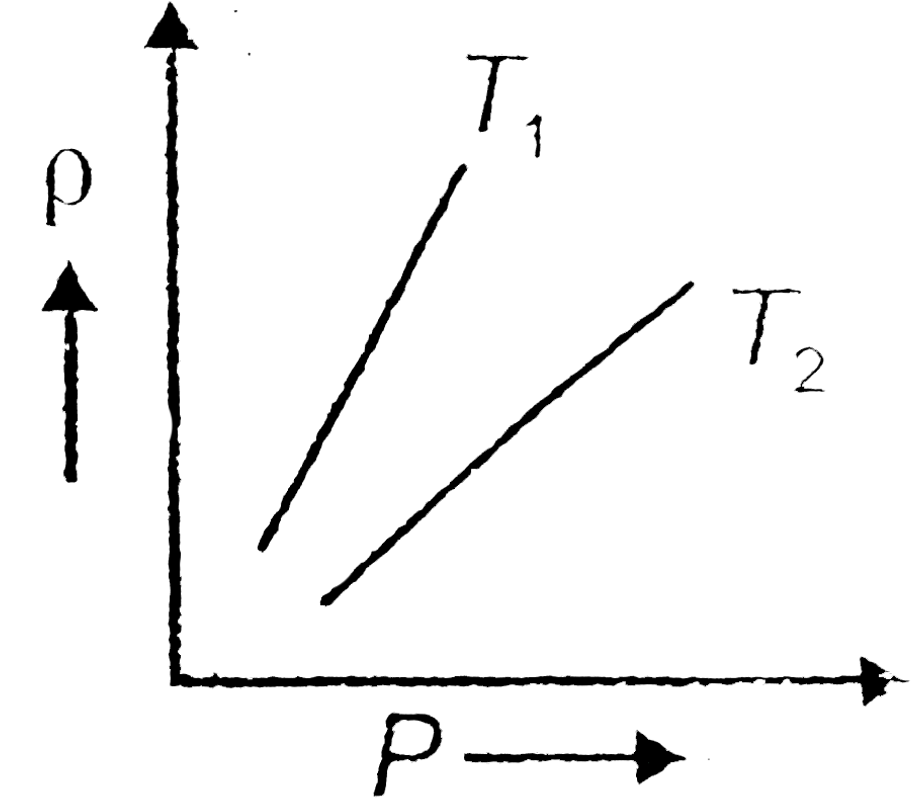
View SolutionThe density (ρ) versus pressure (P) graphs of a given mass of an ideal gas is shown at two temperatures T1andT2. Then relation between T1andT2 may be
View SolutionDensity of gas is inversely proportional to absolute temperature and directly proportional to pressure
⇒d∝PT⇒dTP = constant ⇒d1T1P1=d2T2P2
Density at a particular temperature and pressure can be calculated bousing ideal gas equation
PV=nRT⇒PV=massmolar mass (M)xRT
P×M=massvolume×RT⇒P×M=d×RT
d=PMRT
The density of CO2 at 1 atm and 273K is
View SolutionDensity of gas is inversely proportional to absolute temperature and directly proportional to pressure
⇒d∝PT⇒dTP = constant ⇒d1T1P1=d2T2P2
Density at a particular temperature and pressure can be calculated bousing ideal gas equation
PV=nRT⇒PV=massmolar mass (M)xRT
P×M=massvolume×RT⇒P×M=d×RT
d=PMRT
Which of the following has maximum density?
View SolutionThe degree of dissociation of water in a 0.1M aqueous solution of HCl at a certain temperature t∘C is 3.6×10−15. The temperature t must be : [density of water at t∘C=1gm/mL.]
View Solution
