Four identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.

Let TB be the temperature at B
AB = CD = DE = CF = L & CB = BD = L2
∴FCB=EDB=3L2
Heat flowing per second towards B from E via D is
H1=KA(T2−TB)3L2
Heat flowing per second towards B from F via C is
H2=KA(T3−TB)3L2
Heat flowing per second towards A from B is
H3=KA(TB−T1)L
In steady state, H1+H2=H3
KA(T2−TB)(3L/2)+KA(T3−TB)(3L/2)=KA(TB−T1)L
on solving we get ⇒TB=2T2+2T3+3T17
Similar Questions

Eleven identical rods are arranged as shown in Fig. Each rod has length l, cross sectional area A and thermal conductivity of material k. Ends A and F are maintained at temperatures T1 and T2(<T1), respectively. If lateral surface of each rod is thermally insulated, the rate of heat transfer (dQdt) in each rod is
View SolutionFour thin identical rods AB,AC,BD and EF made of the same material are joined as shown. The free-ends C,D and F are maintained at temperature T1,T2 and T3 respectively. Assuming that there is no loss of heat of the surroundings, the temperature at joint E when the steady state is attained is 1K(2T1+2T2+3T3). Find K(E is mid point of AB)
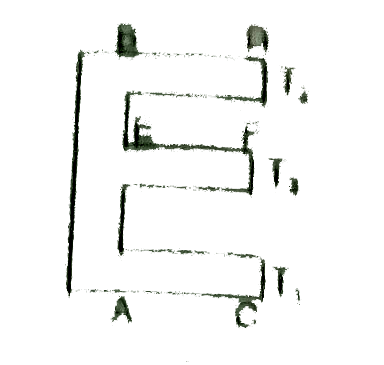
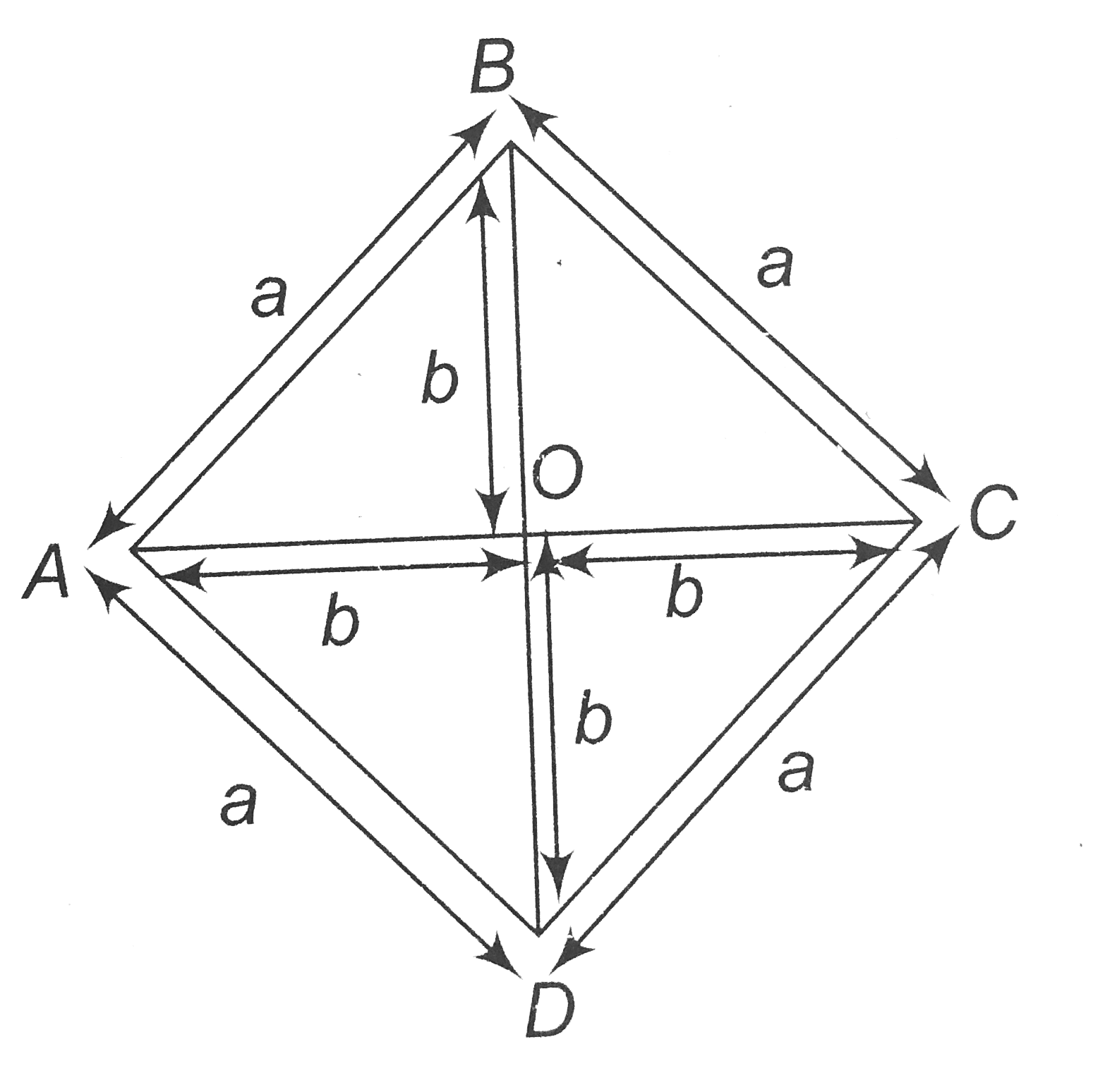
View SolutionAll the rods have same conductance 'K' and same area of cross section 'A'. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct?
View SolutionFive rods of same material and same cross-section are joined as shown. Lengths of rods ab, ad and bc are l, 2l and 3l respectively. Ends a and c are maintained at temperatures 200∘C and 0∘C respectivelly.
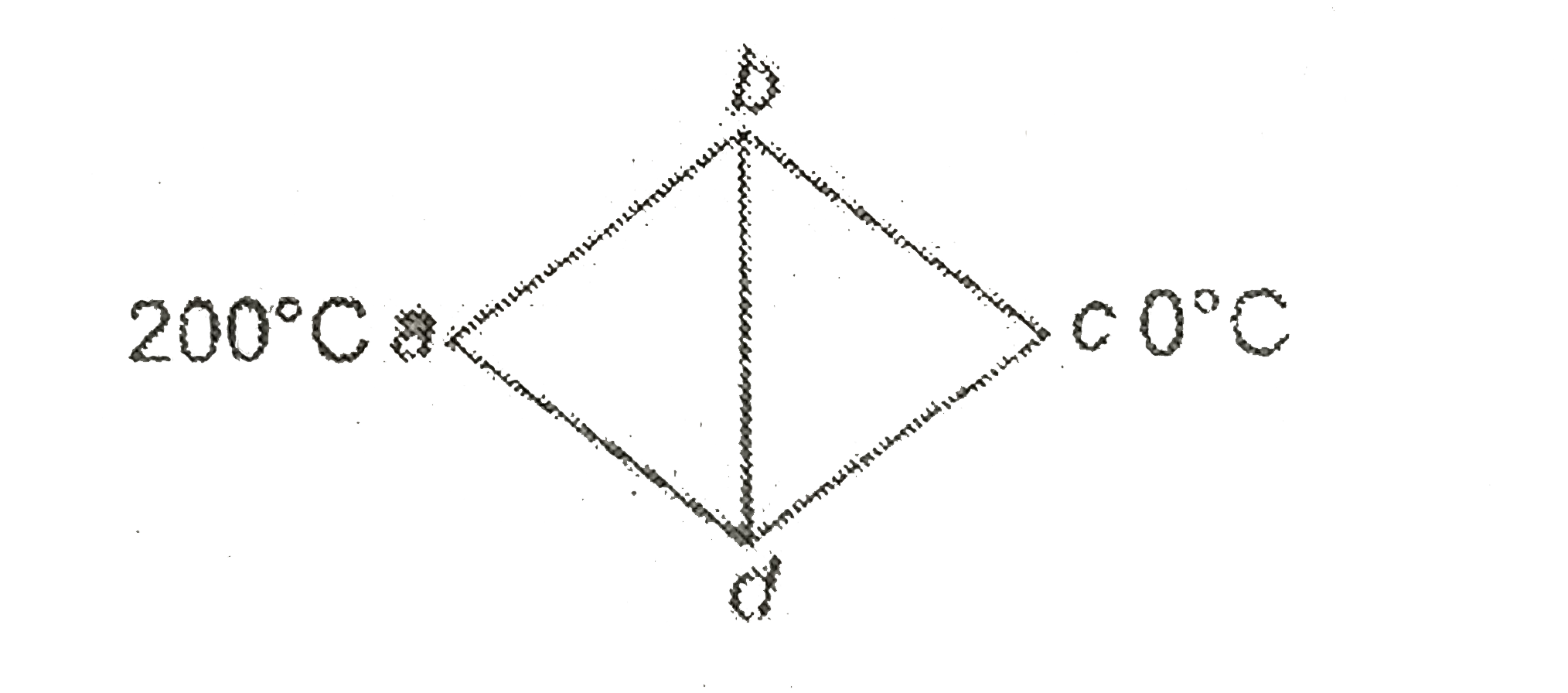
For what length x of rod dc there will be no heat flow through rod bd ?
View SolutionA composite rod made of three rods of equal length and cross-section as shown in fig. The thermal conductivites of the materials of the rods are K/2, 5K and K respectively. The end A and end B are at constant tempertures. All heat entering the face A goes out of the end B there being no loss of heat from the sides of the bar. The effective thermal conductivity of the bar is

View Solution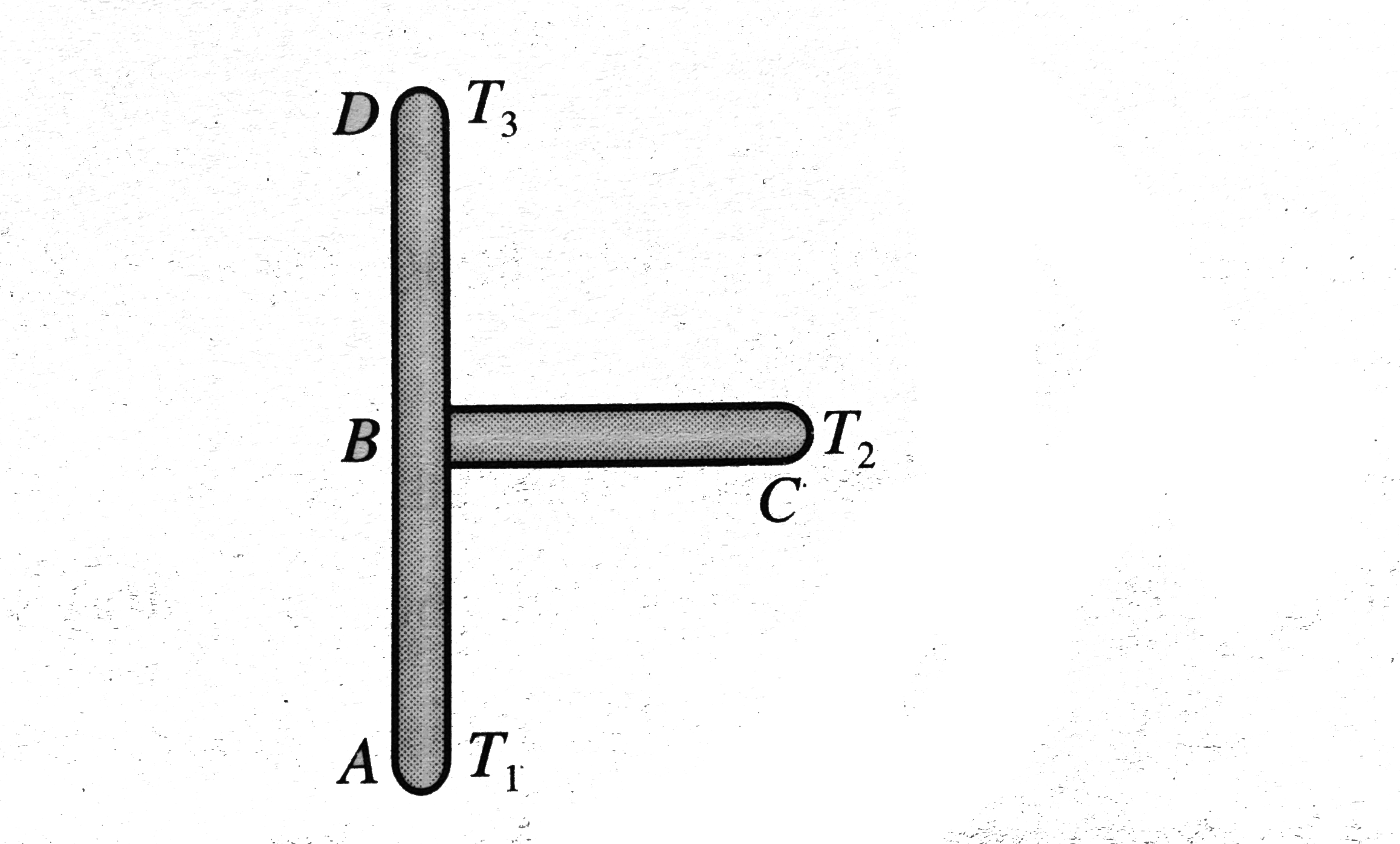
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature T1,T2 and T3 respectively Find the temperature of the junction B. Assume steady state.
View Solution
A circular ring (centre O) of radius a, and of uniform cross section is made up of three different metallic rods AB, BC and CA (joined together at the points A, B and C in pairs) of thermal conductivityies α1,α2 and α3 respectively (see diagram). The junction A, B and C are maintained at the temperatures 100∘C,50∘C and 0∘C, respectively. All the rods are of equal lengths and cross sections. Under steady state conditions, assume that no heat is lost from the sides of the rods. Let Q1,Q2 and Q3 be the rates of transmission of heat along the three rods AB, BC and CA. Then
View Solution
A circular ring (centre O) of radius a, and of uniform cross section is made up of three different metallic rods AB, BC and CA (joined together at the points A, B and C in pairs) of thermal conductivityies α1,α2 and α3 respectively (see diagram). The junction A, B and C are maintained at the temperatures 100∘C,50∘C and 0∘C, respectively. All the rods are of equal lengths and cross sections. Under steady state conditions, assume that no heat is lost from the sides of the rods. Let Q1,Q2 and Q3 be the rates of transmission of heat along the three rods AB, BC and CA. Then
View SolutionSeven rods A, B, C, D, E, F and G are joined as shown in figure. All the rods have equal cross-sectional area A and length l. The thermal conductivities of the rods are KA=KC=K0, KB=KD=2K0, KE=3K0, KF=4K0 and KG=5K0 . The rod E is kept at a constant temperature T1 and the rod G is kept at a constant temperature T2(T2>T1) . (a) Show that the rod F has a uniform temperature T=(T1+2T2)/3 . (b) Find the rate of heat flowing from the source which maintains the temperature T2 .

View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
View Solution
