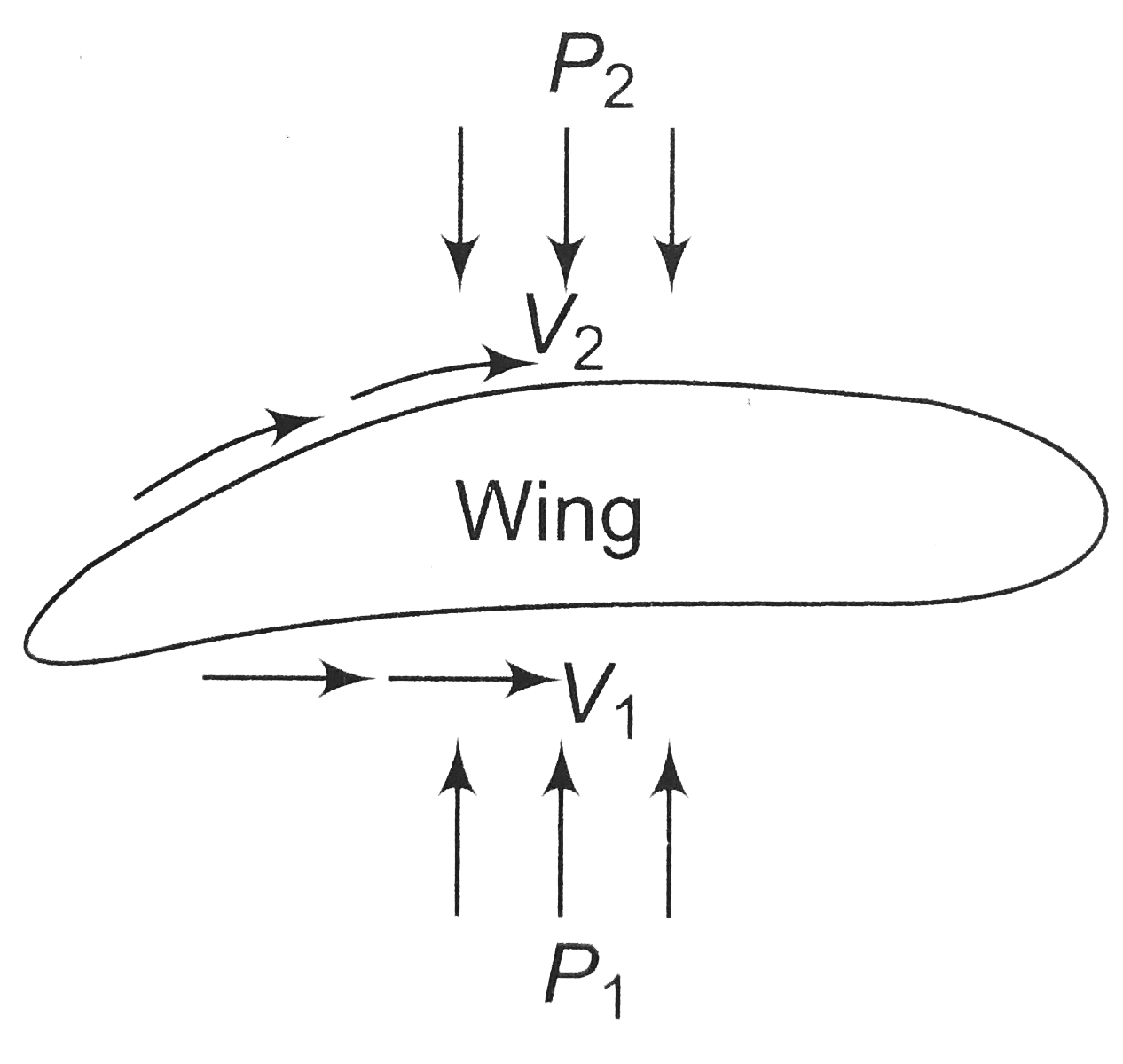
A fully loaded Boeing aircraft has a mass of $3.3 \times 10^{5} k g$ . Its total wing area is $500 m^{2}$ . It is in level flight with a speed of 960 kg/h. (a) estimate the pressure difference between the lower and upper surfaces of the wings (b) estimates the fractional increase in the speed of the air on the upper surface of the wing relative to the lower surface. [the density of air is $ρ = 1.2 k g m^{- 3}$ ].

Video Solution

Text Solution

Verified by Experts

(a) The weight of the Boeing aircraft is balanced by the upward force due to the pressure difference
$Δ P \times A = 3.3 \times 10^{5} k g \times 9.8$
$Δ P = (3.3 \times 10^{5} k g \times 9.8 m s^{- 2}) / 500 m^{2}$
$= 6.5 \times 10^{3} N m^{- 2}$
(b) We ignore the small height difference between the top and bottom sides in Eq. The pressure difference between them is then
$Δ = \frac{ρ}{2} (v_{2}^{2} - v_{1}^{2})$
Where $v_{2}$ is the speed of air over the upper surface and $v_{1}$ is the speed under the bottom surface.
$(v_{2} - v_{1}) = \frac{2 Δ ρ}{ρ (v_{2} + v_{1})}$
Taking the average speed
$v_{a v} = (v_{2} + v_{1}) / 2 = 960 k m / h = 267 m s^{- 1}$ , we have
$(v_{2} - v_{1}) / v_{a v} = \frac{Δ P}{ρ v_{a v}^{2}} \approx 0.08$
The speed above the wing needs to be only 8% higher than that below.

Updated on:21/07/2023

An aircraft of mass $4 \times 10^{5} k g$ with total wing area $500 m^{2}$ in level flight at a speed of 720 $k m h^{- 1}$ . The density of a at its height is $1.2 k g m^{- 3}$ . The fractional increases in the speed of the air on the upper surface of its wings relative to the lower surface is (take $g = 10 m s^{- 2}$ )
A0.04
B0.08
C0.17
D0.34
A plane is in level flight at constant speed and each of its two wings has an area of $25 m^{2}$ . If the speed of the air on the upper and lower surfaces of the wing are $270 k m h^{- 1}$ and '234 km h^(-1)' respectively, then the mass of the plane is (Take the density of the air $= 1 k g m^{- 3}$ )
A1550 kg
B1750 kg
C3500 kg
D3200 kg
In a wind tunnel experiment the pressure on the upper and lower surfaces of the wings are 0.90 $\times 10^{5}$ Pa and 0.91 $\times 10^{5}$ Pa respectively .If the area of the wings is $40 m^{2}$ the net liftng forcw on the wing is
A $2 \times 10^{4}$ N
B $4 \times 10^{4}$ N
C $6 \times 10^{4}$ N
D $8 \times 10^{4}$ N