State Faraday's law of electromagnetic induction.
Figure shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of the paper.The field extends from x=0 to x=b and is zero for x>b.Assume that only the arm PQ posses resistance r.When the arm PQ is pulled outward from x=0 with constant speed v, obtain the expressions for the flux and the induced emf. sketch the variations of these quantities with distance 0≤x≤2b.

Let us first consider the forward motion from x = 0 to x = 2b The flux ϕB . linked with the circuit SPQR is
ϕB=Blx 0≤x<b=Blb b≤x<2b
The induced emf is, ε=−dϕBdt=−Blv 0≤x<b
When the induced emf is nonzero, the current I is I=Blvr (in magnitude)
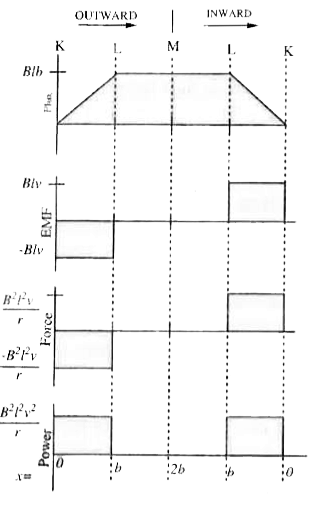
The force required to keep the arm PQ in constant motion is IlB. Its direction is to the left.
F=B2l2vr0≤x<b
F=0b≤x<2b
The Joule heating loss is
Pf=I2r=B2l2v2r0≤x<b
Pi=0b≤x<2b
One obtains similar expressions for the inward motion from x=2b to x=0. One can appreciate the whole process by examining the sketch of various quantities displayed in Fig.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA
58 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB
18 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
Figure shows a rectangular loop conducting PQRS in which the arm PQ is free to move. A uniform magnetic field acts in the direction perpendicular to the plane of the loop. Arm PQ is moved with a valocity v towards the arm RS. Assuming that the arms QR, RS and SP have negligible resistances and the moving arm PQ has the resistance r, obtain the expression for (i) the current in the loop (ii) the force and (iii) the power required to move the arm PQ.

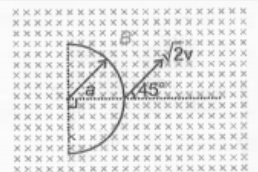
View SolutionA semicircular conducting wire of radius a is moving perpendicular to a uniform magnetic field B with speed√2vas shown in the figure.The emf induced across the wire Is
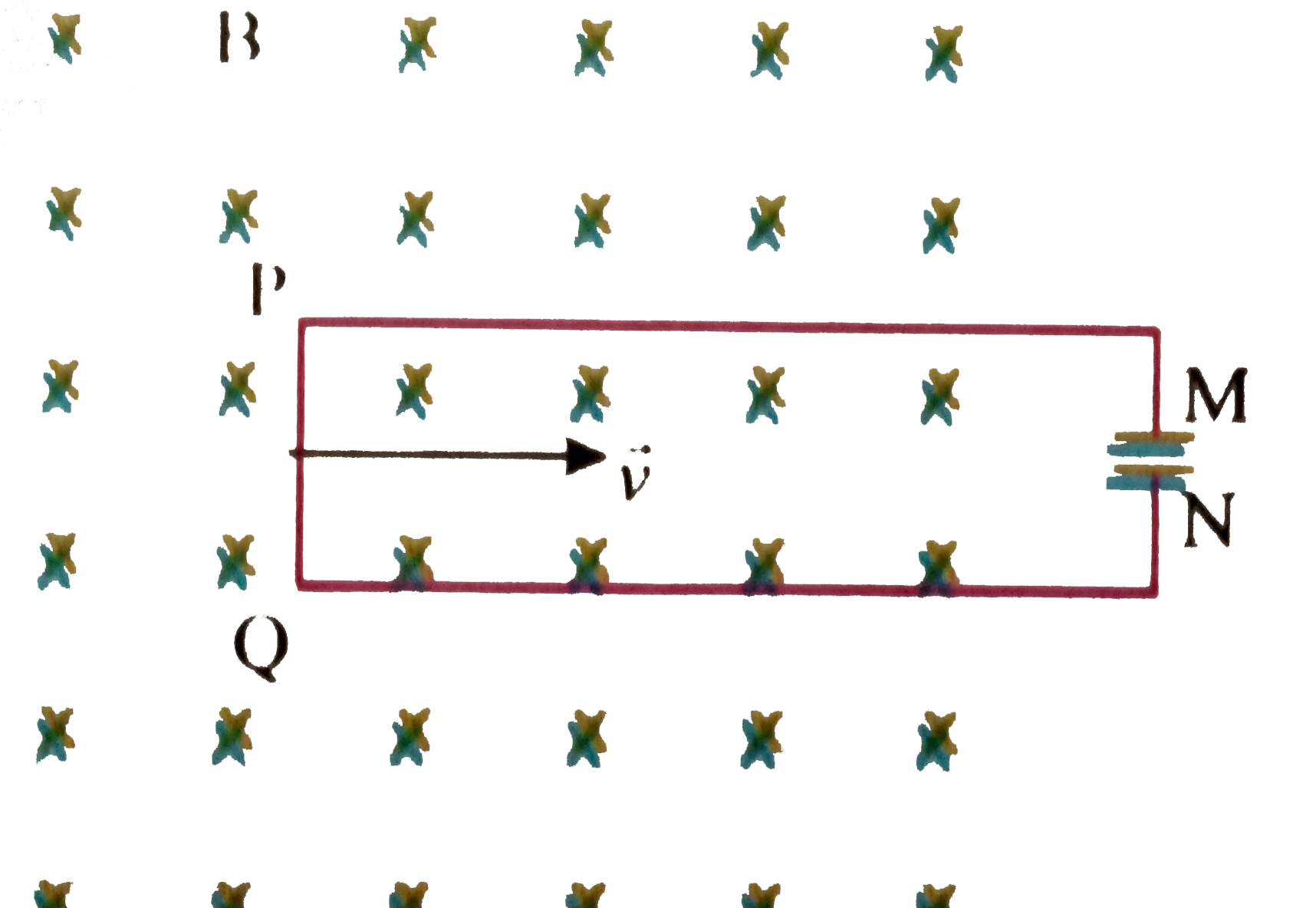
View SolutionA rod PQ is connected to the capacitor plates. The rod is placed in a magnetic field (B) directed downwards perpendicular to the plane of the paper. If the rod is pulled out of magnetic field with velocity →v as shown in Figure.
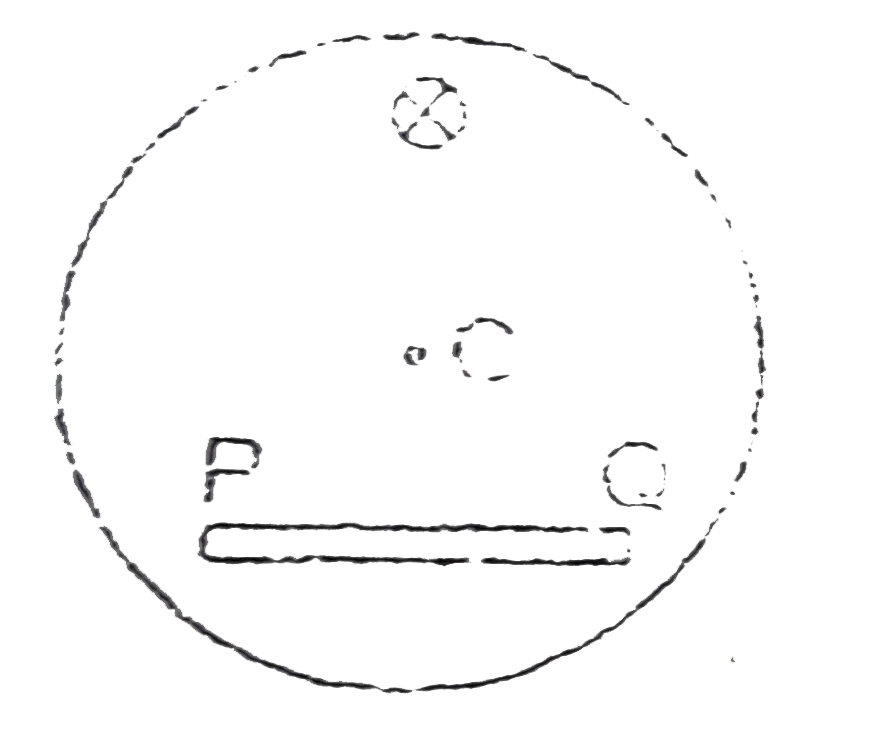
View SolutionIn a cylindrical region uniform magnetic field which is perpendicular to the plane of the figure is in increasing with time and a conducting rod PQ is placed in the region.If C is the centre of the circle then
View SolutionA square loop of side L, resistance R placed in a uniform magnetic field B acting normally to the plane of the loop. If we attempt to pull it out of the field with a constant velocity v, then the power needed is
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionRod PQ of length 2l is rotating about its midpoint C in a uniform magnetic field B which is perpendicular to the plane of rotation of the rod . Find the induced emf between PQ and PC. Draw the circuit diagram of parts PC and CQ.

View SolutionA rectangular loop with a sliding conductor of length l is located in a uniform magnetic field perpendicular to the plane of the loop . The magnetic induction is b. The resistances R1 and R2, respectively. Find the current through the conductor during its motion to the right with a constant velocity v.

View SolutionMagnetic field at point O due to straight conductor PQ is
_PHY_E06_180_Q01.png)
View SolutionA metallic ring (radius R) of negligible resistance has a resistance r connected across its diameter as shown in the figure. It is moving with velocity v0 in a constant magnetic field B0 acting perpendicular to the plane of the paper in the inward direction. The current in the resistance is :
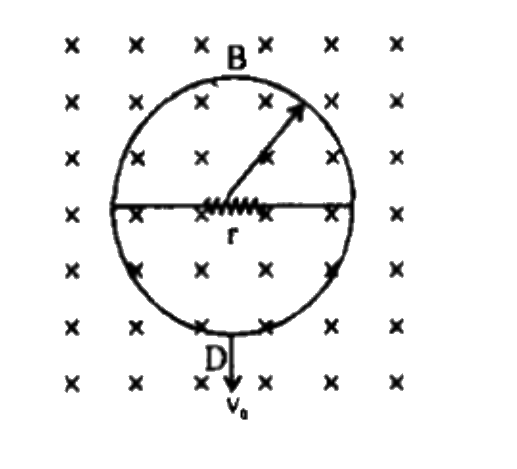
View Solution
