In U - V method, the object distance is 30.0cm and image distance is 60.0cm from pole of concave mirror. The percentage error in measurement of focal length of mirror is n18%. Find the value of n
5
4
3
2
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- Object distance (u) = -30.0 cm (negative for concave mirror)
- Image distance (v) = -60.0 cm (negative for concave mirror)
Step 2: Use the mirror formula
The mirror formula is given by:
1f=1v+1u
Substituting the values of u and v:
1f=1−60+1−30
Step 3: Calculate the focal length (f)
Calculating the right-hand side:
1f=−160−130
Finding a common denominator (which is 60):
1f=−160−260=−360=−120
Thus, the focal length f is:
f=−20 cm
Step 4: Differentiate the mirror formula
To find the percentage error in the focal length, we differentiate the mirror formula:
ddf(1f)=ddv+ddu
This gives:
−dff2=dvv2+duu2
Step 5: Substitute the errors
Let Δu and Δv be the errors in the measurements of u and v. Assuming the least count of the measuring instrument is 0.1 cm:
Δu=0.1 cm,Δv=0.1 cm
Substituting these values into the differentiated equation:
−Δff2=0.1(−60)2+0.1(−30)2
Calculating the right-hand side:
−Δff2=0.13600+0.1900
Finding a common denominator (which is 3600):
−Δff2=0.13600+0.43600=0.53600
Step 6: Solve for Δf
Now, substituting f=−20:
−Δf(−20)2=0.53600
Calculating:
−Δf400=0.53600
Cross-multiplying gives:
Δf=−0.5×4003600
Thus:
Δf=−2003600=−118 cm
Step 7: Calculate the percentage error
The percentage error in the focal length is given by:
Percentage error=(Δff)×100
Substituting the values:
Percentage error=⎛⎝11820⎞⎠×100=100360=518%
Step 8: Identify n
From the problem, the percentage error is given as n18%. Therefore, we have:
n18=518
Thus, n=5.
Final Answer
The value of n is 5.
---
- Object distance (u) = -30.0 cm (negative for concave mirror)
- Image distance (v) = -60.0 cm (negative for concave mirror)
The mirror formula is given by:
1f=1v+1u
Substituting the values of u and v:
1f=1−60+1−30
Calculating the right-hand side:
1f=−160−130
Finding a common denominator (which is 60):
1f=−160−260=−360=−120
Thus, the focal length f is:
f=−20 cm
To find the percentage error in the focal length, we differentiate the mirror formula:
ddf(1f)=ddv+ddu
This gives:
−dff2=dvv2+duu2
Let Δu and Δv be the errors in the measurements of u and v. Assuming the least count of the measuring instrument is 0.1 cm:
Δu=0.1 cm,Δv=0.1 cm
Substituting these values into the differentiated equation:
−Δff2=0.1(−60)2+0.1(−30)2
Calculating the right-hand side:
−Δff2=0.13600+0.1900
Finding a common denominator (which is 3600):
−Δff2=0.13600+0.43600=0.53600
Now, substituting f=−20:
−Δf(−20)2=0.53600
Calculating:
−Δf400=0.53600
Cross-multiplying gives:
Δf=−0.5×4003600
Thus:
Δf=−2003600=−118 cm
The percentage error in the focal length is given by:
Percentage error=(Δff)×100
Substituting the values:
Percentage error=⎛⎝11820⎞⎠×100=100360=518%
From the problem, the percentage error is given as n18%. Therefore, we have:
n18=518
Thus, n=5.
The value of n is 5.
Topper's Solved these Questions
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
4 Videos
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
4 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - Exercise -I
10 Videos
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)
60 Videos
Similar Questions
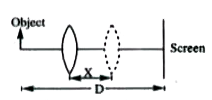
Displacement method is applicable to determine the focal length of convex lens. In this method, the applicable formula is f=D2−X24D. Here D= distance between object plane and screen on which image is formed f= focal length of lens, X= distance between two position of lens. To determine focal length of lens, the measure value of D and x are 90.0cm and 30.0cm, respectively. If percentage error in measurement of focal length is n×10−1%. Find the value of n.
View SolutionFor an object placed at a distance 20 cm from a concave mirror, the image is formed at the same position. What is the focal length of the mirror?
View Solution
Knowledge Check
An object 2cm high is placed at a distance of 16cm from a concave mirror, which produces a real image 3cm high. What is thr focal length of the mirror ? Find the position of the image ?
A−9.6cmB−3.6cmC−6.3cmD−8.3cm
An object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionAn object is placed at a distance 20 cm from the pole of a convex mirror of focal length 20 cm. The image is produced at
View SolutionThe distance of an object from a concave spherical mirror is equal to the focal length of the mirror. Then the image.
View SolutionAn object is placed at a distance f in the front of a convex mirror. If focal length of the mirror is f, then distance of image from pole of the mirror is
View SolutionAn object is placed at a distance of 20 cm from a concave mirror of focal lenght 10 cm. What is the image distance?
View SolutionWhen an object of height 1 cm its kept at a distance 4 cm from a concave mirror, its erect image of height 1.5 cm is formed at a distance 6 cm behind the mirror. Find the focal length of mirror.
View SolutionAn object is placed at 6 cm distance in front of a concave mirror of focal length 4 cm.
What will be the nature of the image?
View Solution
