The AM wave of equivalent to the summation of
two sinusoidal waves
three sinusoidal waves
four sinusoidal waves
none of these
The correct Answer is:B
To determine how many sinusoidal waves an amplitude modulated (AM) wave is equivalent to, we can analyze the components of an AM wave step by step.
1. Understanding AM Wave Components:
An AM wave consists of a carrier wave and a modulating signal. The modulating signal can be represented as:
m(t)=Amsin(ωmt)
where Am is the amplitude of the modulating signal and ωm is its angular frequency.
2. Carrier Wave Representation:
The carrier wave can be expressed as:
c(t)=Acsin(ωct)
where Ac is the amplitude of the carrier wave and ωc is its angular frequency.
3. Combining the Waves:
The AM wave can be represented as:
AM(t)=(Ac+m(t))⋅sin(ωct)
Substituting m(t) into the equation gives:
AM(t)=(Ac+Amsin(ωmt))⋅sin(ωct)
4. Expanding the Equation:
Expanding this expression leads to:
AM(t)=Acsin(ωct)+Amsin(ωmt)sin(ωct)
5. Using Trigonometric Identities:
We can use the trigonometric identity:
2sinAsinB=cos(A−B)−cos(A+B)
to rewrite the product Amsin(ωmt)sin(ωct):
Amsin(ωmt)sin(ωct)=Am2(cos((ωc−ωm)t)−cos((ωc+ωm)t))
6. Final Expression:
Thus, the complete expression for the AM wave becomes:
AM(t)=Acsin(ωct)+Am2cos((ωc−ωm)t)−Am2cos((ωc+ωm)t)
This shows that the AM wave consists of:
- One carrier wave
- Two additional sidebands (resulting from the modulation)
7. Counting the Sinusoidal Waves:
Therefore, the total number of sinusoidal waves in an AM wave is:
- 1 (carrier wave)
- 2 (sidebands)
This results in a total of 3 sinusoidal waves.
Conclusion:
The AM wave is equivalent to the summation of three sinusoidal waves.
An AM wave consists of a carrier wave and a modulating signal. The modulating signal can be represented as:
m(t)=Amsin(ωmt)
where Am is the amplitude of the modulating signal and ωm is its angular frequency.
The carrier wave can be expressed as:
c(t)=Acsin(ωct)
where Ac is the amplitude of the carrier wave and ωc is its angular frequency.
The AM wave can be represented as:
AM(t)=(Ac+m(t))⋅sin(ωct)
Substituting m(t) into the equation gives:
AM(t)=(Ac+Amsin(ωmt))⋅sin(ωct)
Expanding this expression leads to:
AM(t)=Acsin(ωct)+Amsin(ωmt)sin(ωct)
We can use the trigonometric identity:
2sinAsinB=cos(A−B)−cos(A+B)
to rewrite the product Amsin(ωmt)sin(ωct):
Amsin(ωmt)sin(ωct)=Am2(cos((ωc−ωm)t)−cos((ωc+ωm)t))
Thus, the complete expression for the AM wave becomes:
AM(t)=Acsin(ωct)+Am2cos((ωc−ωm)t)−Am2cos((ωc+ωm)t)
This shows that the AM wave consists of:
- One carrier wave
- Two additional sidebands (resulting from the modulation)
Therefore, the total number of sinusoidal waves in an AM wave is:
- 1 (carrier wave)
- 2 (sidebands)
The AM wave is equivalent to the summation of three sinusoidal waves.
Topper's Solved these Questions
- COMMUNICATION SYSTEM Book:AAKASH SERIESChapter:COMMUNICATION SYSTEM Exercise:LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - IV) (Straight Objective & More than one Correct Answer Type Questions)
Explore 20 Videos
- COMMUNICATION SYSTEM Book:AAKASH SERIESChapter:COMMUNICATION SYSTEM Exercise:LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - II) (Straight Objective & More than one Correct Answer Type Questions)
Explore 19 Videos
- CAPACITORS Book:AAKASH SERIESChapter:CAPACITORS Exercise:PRACTICE SHEET (ADVANCED) (Integer Type Questions)
Explore 2 Videos
- COMMUNICATION SYSTEMS Book:AAKASH SERIESChapter:COMMUNICATION SYSTEMS Exercise:PRACTICE EXERCISE (TV Antenna)
Explore 16 Videos
Similar Questions
Knowledge Check
An ovule is an equivalent of:
AmegasporangiumBmegasporophyllCmegasporeDfemale gamete
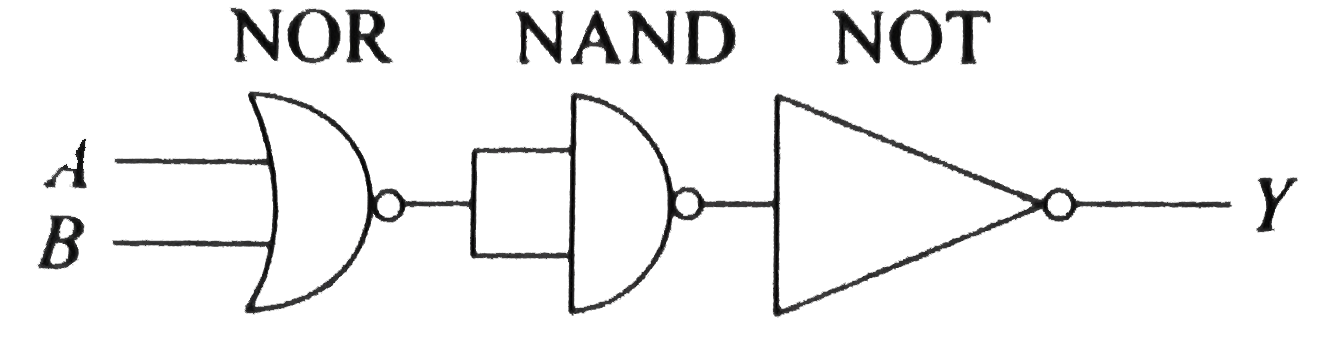
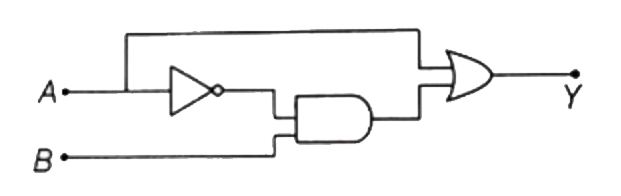
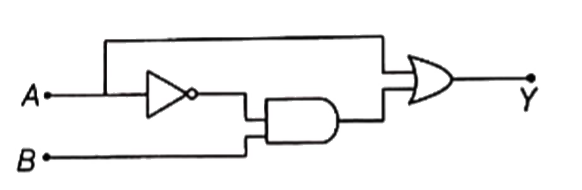
The circuit is equivalent to
View SolutionThe major product of the following reaction is:
CH3−CH3∣C∣H−CHCH3∣BrCH3OH−−−−→
View SolutionStatement-1 : Interference pattern for two light waves can be explained using conservation of energy.
Statement-2 : Intensities at maxima is greater than the summation of intensities of two individual waves.
View SolutionA carrier wave of frequency 1.5 MHz and amplitude 50 V is modulated by a sinusoidal wave of frequency 10KHz producing 50% amplitude modulation. Calculate the amplitude of the AM wave and frequencies of the side bands produced.
View SolutionThe path difference equivalent to a phase difference of 180∘ (given wavelength of wave = λ) is
View SolutionA solenoid of radius 4 cm and 1000 turns , carries a current of 8 A. If it is equivalent to a magnet of same size and magnetisation →M (Magnetic moment / Volume) of 20000Am−1 , then the length of the solenoid is
View SolutionThe union of two equivalence relations on a set is not necessarily an equivalence relation on the set.
View Solution