A sky wave with a frequency 55 MHz is incident on D-region of the earth.s atmosphere at 45∘. The angle of refraction is (electron density for D-region is 400 electron/c.c)
60∘
45∘
30∘
15∘
The correct Answer is:B
To solve the problem of finding the angle of refraction for a sky wave with a frequency of 55 MHz incident on the D-region of the Earth's atmosphere at an angle of 45 degrees, we can follow these steps:
Step 1: Convert Electron Density
The electron density given is 400 electrons/cm³. We need to convert this to electrons/m³.
ρ=400 electrons/cm3=400×106 electrons/m3=4×108 electrons/m3
Step 2: Identify the Incident Angle
The angle of incidence i is given as 45 degrees.
Step 3: Determine the Refractive Index of Air
The refractive index of air N1 is approximately 1.
Step 4: Calculate the Refractive Index of the D-region
Using the formula for the refractive index N2 of the D-region:
N2=N1√1−81.45×ρf2
Where:
- ρ=4×108 electrons/m3
- f=55 MHz=55×106 Hz
Substituting the values:
N2=1√1−81.45×4×108(55×106)2
Calculating (55×106)2:
(55×106)2=3025×1012=3.025×1015
Now substituting back into the equation for N2:
N2=1√1−81.45×4×1083.025×1015
Calculating the fraction:
81.45×4×1083.025×1015=325.8×1083.025×1015=325.83.025×10−7≈1.075×10−7
Thus,
N2≈1√1−1.075×10−7≈1 (since the term is very small)
Step 5: Apply Snell's Law
According to Snell's Law:
N1sin(i)=N2sin(r)
Substituting N1=1 and N2≈1:
sin(45∘)=sin(r)
Since sin(45∘)=√22, we have:
sin(r)=√22
Step 6: Conclusion
This means that the angle of refraction r is also 45 degrees.
r=45∘
Final Answer
The angle of refraction is 45∘.
---
The electron density given is 400 electrons/cm³. We need to convert this to electrons/m³.
The angle of incidence i is given as 45 degrees.
The refractive index of air N1 is approximately 1.
Using the formula for the refractive index N2 of the D-region:
- ρ=4×108 electrons/m3
- f=55 MHz=55×106 Hz
According to Snell's Law:
This means that the angle of refraction r is also 45 degrees.
The angle of refraction is 45∘.
Topper's Solved these Questions
- COMMUNICATION SYSTEM BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEM EXERCISE - LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - II) (Straight Objective & More than one Correct Answer Type Questions)
19 Videos
- COMMUNICATION SYSTEM BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEM EXERCISE - LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - III) (Straight Objective & More than one Correct Answer Type Questions)
26 Videos
- CAPACITORS BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (ADVANCED) (Integer Type Questions)
2 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
Similar Questions
What is the value of frequency at which electromagnetic wave must be propagated for the D - region of atmosphere to have a refractive index of 0.5. Electron density for D - region is 400 electrons/c.c.
View SolutionAt constant pressure the r.m.s. velocity c is related to density d as
View SolutionA ray of light is normally incident on one face of an equilateral glass prism. Answer the following :
(a) What is the angle of incidence on the first face of the prism?
(b) What is the angle of refraction from the first face of the prism ?
(c) What will be the angle of incidence at the second face of the prism ?
(d) Will the light ray suffer minimum deviation by the prism ?
View SolutionAn eletromagnetic wave of frequency 28 MHz passes through the lower atmosphere of earth and gets incident on the ionosphere.Shall the ionosphere reflects these waves?
View SolutionCalculated the phase velocity of electromagnetic wave having electron density and frequency for D-layer : (N = 400 electrion/cc and v = 300 kHz)
View SolutionThe maximum fequency for reflection of sky waves from a certain layer of the ionosphere is found to be fmax=9(Nmax)1/2, Where N _max is the maximum electron density at that layer of the ionosphere.On a certain day it is observed that signals of frequencies higher than 5 MHz are not received by reflection from the F1 layer of the ionosphere while signals of frequencies higher than 8 MHz are not received by reflection from the F2 layer of the ionosphere. Estimate the maximum electron densities of the F1 and F2 layers on that day.
View SolutionFor sky wave propagation of a 10MHz signal, what should be the minimum electron density in ionosphere?
View SolutionThe probability density plots of 1s and 2s atomic orbitals are given in figures.
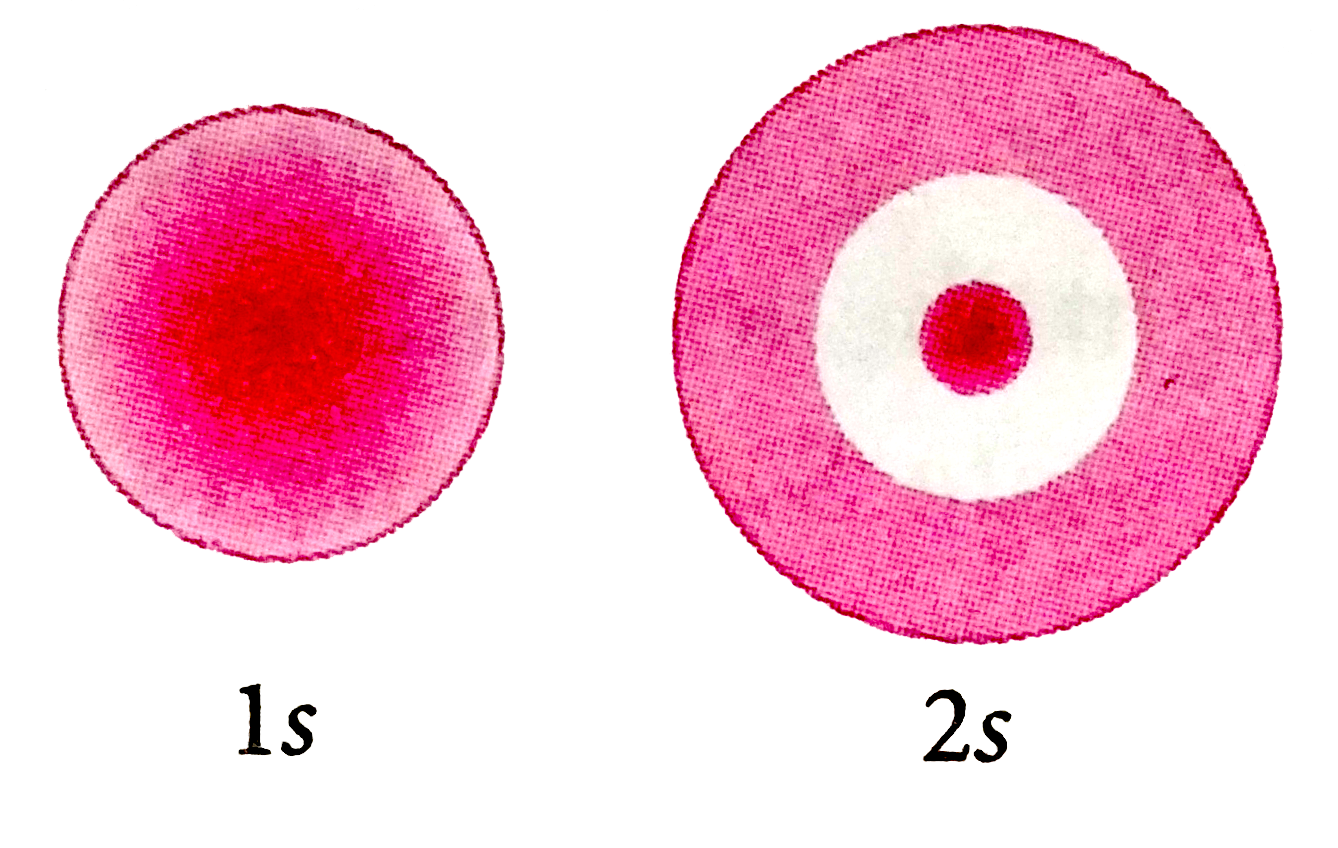
The density of dots in a region represents the probability density of finding electrons in the region. On the basis of the above diagram, which of the following statements is incorect?
View SolutionA source S and a detector D high frequency waves are a distance d apart on the ground. The direct wave from S is found to be in phase at D with the wave from S that is reflected from horizontal layer at an altitude H. The incident and reflected rayes make the same angle with the reflecting layer. When the layer rises a distance h, no signal is detected at D . Negle ct absorption in the atmosphere and find the relation between d,h, H and the wavelength λ of the waves.

View SolutionDraw a diagram to show refraction through a glass slab and label the following: (a) incident ray (b) refracted ray (c) emergent ray (d) angle of incidence (e) angle of refraction at the first boundary of two mediums (f) angle of emergence and (g) lateral displacement
View Solution
