A sonometer wire resonates with a given tuning fork forming standing waves with three antinodes between the two bridges when a mass of 16 Kg is suspended from the wire. When this mass is replaced by a mass .9 kg. the wire resonates with the same tuning fork for .p. antinodes for the same positions of the bridges. Then .p. is
The correct Answer is:4
To solve the problem, we need to analyze the relationship between the mass suspended from the sonometer wire and the number of antinodes formed when the wire resonates with a tuning fork.
1. Understanding the Problem:
- We have a sonometer wire that resonates with a tuning fork, forming standing waves with 3 antinodes (P1 = 3) when a mass of 16 kg (M1 = 16 kg) is suspended from it.
- When this mass is replaced with a mass of 9 kg (M2 = 9 kg), we need to find the new number of antinodes (P2 = P).
2. Using the Formula for Frequency:
- The frequency of the standing wave in the wire is given by the formula:
f=P2L√Tμ
- Here, T is the tension in the wire, μ is the mass per unit length of the wire, and L is the length of the wire.
3. Setting Up the Tension:
- The tension in the wire due to the suspended mass is given by:
T=M⋅g
- For the first case (with 16 kg):
T1=M1⋅g=16g
- For the second case (with 9 kg):
T2=M2⋅g=9g
4. Equating Frequencies:
- Since the frequency must be the same for both cases (as the same tuning fork is used), we can set up the equation:
P12L√T1μ=P22L√T2μ
- Canceling 2L and μ from both sides, we have:
P1√T1=P2√T2
5. Substituting Values:
- Substitute P1=3, T1=16g, and T2=9g:
3√16g=P√9g
- Simplifying gives:
3⋅4√g=P⋅3√g
6. Solving for P:
- Dividing both sides by 3√g:
12=P
- Thus, P=4.
Final Answer:
The value of P is 4.
- We have a sonometer wire that resonates with a tuning fork, forming standing waves with 3 antinodes (P1 = 3) when a mass of 16 kg (M1 = 16 kg) is suspended from it.
- When this mass is replaced with a mass of 9 kg (M2 = 9 kg), we need to find the new number of antinodes (P2 = P).
- The frequency of the standing wave in the wire is given by the formula:
f=P2L√Tμ
- Here, T is the tension in the wire, μ is the mass per unit length of the wire, and L is the length of the wire.
- The tension in the wire due to the suspended mass is given by:
T=M⋅g
- For the first case (with 16 kg):
T1=M1⋅g=16g
- For the second case (with 9 kg):
T2=M2⋅g=9g
- Since the frequency must be the same for both cases (as the same tuning fork is used), we can set up the equation:
P12L√T1μ=P22L√T2μ
- Canceling 2L and μ from both sides, we have:
P1√T1=P2√T2
- Substitute P1=3, T1=16g, and T2=9g:
3√16g=P√9g
- Simplifying gives:
3⋅4√g=P⋅3√g
- Dividing both sides by 3√g:
12=P
- Thus, P=4.
The value of P is 4.
Similar Questions
A sonometer wire resonates with a given tuning fork forming standing waves with five antitodes between the two bridges when a mass of 9kg is suspended from the wire. when this same tuning fork forming three antitodes for the same positions of the bridges. the value of M is
View SolutionA wire longates by 9 mm when a load of 10kg is suspended from it. What is the elongation when its radius is doubled, iff all other quantities are same as before ?
View Solution
Knowledge Check
A metal wire of length L1 and area of cross section A is attached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
A[(Y1Y2)A][2(Y1L2+Y2L1)]B[(Y1Y2)A](L1L2)2C[(Y1Y2)A](Y1L2+Y2L1)D[(Y1Y2)1/2A](L2+L1)1/2A metal wire of length L1 and area of cross section A is ttached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
AY1Y2A2(Y1L2+Y2L1)BY1Y2A(L1L2)1/2CY1Y2A(Y1L2+Y2L1)D(Y1Y2)1/2A(L1L2)1/2
A tuning fork is in unison with 1.0 m length of sonometer wire. When the stretching weights are immersed in water, the length of the wire in unison with the same tuning fork is 0.934 m. Calculate the density of the material of the weights ?
View SolutionA sonometer wire is under a tension of 10 N and the length between the bridges is 2m. A metre long wire of sonometer has mass of 1.0 gm. Deduce the speed of transverse wave and the frequency of 1st hormonic.
View Solution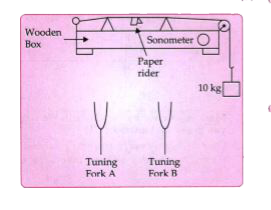
The diagram above shows a wire stretched over a sonometer. Stems of two vibrating tuning forks A and B are touched to the wooden box of the sonometer. It is observed that the paper rider (a small piece of paper folded at the centre) present on the wire flies off when the stem of vibrating tuning fork B is touched to the wooden box but the paper just vibrates when the stem of vibrating tuning fork A is touched to the wooden box.
Why does the paper rider fly off when the stem of tuning fork B is touched to the box ?
View SolutionThe diagram below shows a wire stretched over a sonometer. Stems of two vibrating tuning forks A and B are touched in turn to the wooden box of the sonometer. It is observed that the paper rider (a small piece of paper folded at the centre) present on the wire flies off when the stem of vibrating tuning fork B is touched to the wooden box but the paper just vibrates when the stem of vibrating tuning fork A is touched to the wooden box.
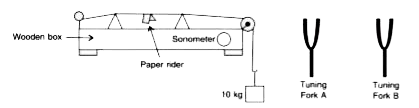
Name the phenomenon when the paper rider just vibrates.
View Solution
The diagram above shows a wire stretched over a sonometer. Stems of two vibrating tuning forks A and B are touched to the wooden box of the sonometer. It is observed that the paper rider (a small piece of paper folded at the centre) present on the wire flies off when the stem of vibrating tuning fork B is touched to the wooden box but the paper just vibrates when the stem of vibrating tuning fork A is touched to the wooden box.
Name the phenomenon when the paper rider flies off.
View SolutionA wire gets elongated by 4 mm when a block of mass 2 kg is suspended from it. Now, the block is immersed in water, the wire contracts by 1 mm. Find the density of block when the density of water is 1000kg/m3.
View Solution

